To purchase the print book Delineating the Horoscope click here

Subheadings:  Events Are Attracted Only by Increased Activity of Thought Cells    Character Vibrations    Signs    Planets    Aspects    Friends    Hopes    Disappointments    Studies, Writing, Publishing, Brethren    Religion    Secret Enemies and the Influence of Astrals    Open-Enemies    Journeys

Birth Charts:  Pat O’Brien    Sir Arthur Conan Doyle    Professor A. Van der Nailen

Chapter 6

Friends, Enemies and Associates

THE power of the various objects and persons which an individual contacts to influence his life and destiny either in the direction he desires or contrary to his wishes, is determined by the amount and kind of energy they contribute to definite groups of thought cells within his astral body. The control of his life, and its most effective direction into the channels of his choosing, therefore, must include an intelligent selection of friends and inanimate associates.

Whether animate or inanimate, whether a musical tone or an unspoken thought, each close associate radiates astral energy the quality of which may be determined. This invisible energy finds its way, over the stellar aerials which span the astral body of man, to the stellar cells within, and adds its activities to such of them as it thus reaches.

These stellar cells, and the thought structures they compose, are located in the particular compartment of the astral body relating to the department of life about which the thoughts, impulses and emotions which furnished their substance had their origin. And when they are furnished with additional energy from planets, from the thoughts of the individual, or from the character vibrations of such associates as we arc now considering, they work, with such subjective intelligence as they possess, to attract into the life events relating to this department of life.

That is, stellar cells having had their origin in impulses relating to personal property, when they are given new energy, work to attract into the life events having to do with money. And stellar cells having had their origin in feelings about friendship, when energy enough is afforded them bring into the life events relating to friendship. The compartments of the astral body where stellar cells and stellar structures are located, according to the department of their origin, are mapped by the houses of the birth chart.

Astral energy from planets, thoughts, or character vibrations can only reach the thought cells within any particular compartment of the astral body in unusual volume through being picked up, radio fashion, by one of the stellar aerials, mapped by an aspect, which traverses the astral body. These stellar aerials lead directly into certain compartments and not into other compartments. The energy thus picked up by such an aerial flows readily into the compartments mapped by its planetary terminals. And through sympathetic response it is able to reach, although in a minor degree of volume, the stellar cells in the compartments ruled by the planets which map its terminals.

Caruso’s famous, and oft’ repeated café demonstration with a wine glass illustrates this principle of sympathetic response. Entering a café he would call for a glass, tap it to get its tone, and instruct the waiter to place it on the farther side of the room. Then, with his vibrant voice sounding the same tone, the wine glass across the room would be shattered. In a less dramatic way the response of a piano string, when its tone is sounded on some other instrument in the same vicinity, also affords a parallel example.

Any stellar aerial, either permanent as mapped by an aspect in the birth chart or temporary as mapped by a progressed aspect, is capable of picking up only astral energy of the vibratory rates corresponding to the two planets which map its terminals. If there is an aspect between Mars and Saturn, for instance, the stellar aerial so mapped has the ability to pick up either Mars vibratory rates or Saturn vibratory rates, but is unable to pick up the vibratory rates of the Sun, Venus, or Jupiter.

Furthermore, which is most important, whatever Mars energy or whatever Saturn energy is picked up from any source by such an aerial is given either a harmonious quality or a quality of discordant static, according to the length of the aerial as mapped by the aspect.

Whatever comes in over an aerial mapped by a square aspect, for instance, is given so much discord by the aerial that when it reaches the stellar cells of the compartments where its terminals are located they are made to feel intensely uncomfortable. Prodded to activity in a most disagreeable way they move, in their inner-plane manner, to bring an obstacle into the life relating to their department. That is, if they are located in the eleventh compartment, the obstacle will arise from friends; but if they are located in the second compartment, the obstacle will be to the making or retaining of money.

If, therefore, we possess a knowledge of the vibratory quality, or planetary rulership, of the various things we contact, and the birth chart of an individual, we are in a position to determine how associating with any particular thing will influence him.

Vibratory rates which must reach the thought cells of his astral body over an aerial which gives them discordant static are inclined to attract to him only disagreeable events. But vibratory rates which must reach the thought cells of his astral body over an aerial which gives them a harmonious trend are inclined to attract to him fortunate conditions.

Events Are Attracted Only by Increased Activity of Thought Cells

And the department of life chiefly thus influenced, either for fortune or misfortune, is the one the stellar cells of which are given the greatest activity by the new energy received.

Aside from aerials leading into them the zones of the astral body mapped by the signs of the zodiac each have a characteristic resonance. They are thus, as explained, influenced through sympathetic response. And this sympathetic response is not merely to the energy coming in over the aerial one terminal of which is mapped by the ruling planet of the sign, but also to the thought vibrations and character vibrations of the same rate as the sign.

If, for instance, an individual is closely associated with things ruled by the sign Aries, the whole zone of the astral body mapped by the sign Aries responds to the vibrations of these Aries things. The stellar cells thus, through sympathetic response, gain new energy and become more active. But, because Aries energy is also received by the stellar aerial which has Mars as one terminal, the sympathetic response to this Mars aerial tends to determine whether the activity thus stimulated is one of harmony or one of discord.

The most active and highly organized stellar structures in any compartment of the astral body are mapped by planets. Wherever a planet is located in the birth chart is a group of thought cells in a high state of activity. The major thought element of which they are composed belongs to the family ruled by the planet thus mapping them. They form the terminal in the astral body for such aerials as are Indicated by the aspects of this planet.

Because of their organization as a dynamic stellar structure, and the energy they receive from the aerials for which they act as a terminal, they have much more power and more readily become active than the other cells in the same compartment not mapped by a planet. Yet when the stellar cells surrounding them become active due to energy received by sympathetic response, either to the vibrations of objects ruled by the sign, or to energies picked up by an aerial mapped by any aspect to the planet ruling the sign, this activity is communicated by direct contact to the dynamic stellar structures mapped by planets in the sign.

Because the thought cells mapped by a planet in the sign are so much more vigorous, any activity imparted to the stellar cells of the compartment mapped by a sign, even more profoundly affects the group of thought cells thus acting as the terminal for an aerial. The energy is conveyed to them by direct contact with other stellar cells in the same zone; and because of their greater vigor what they accomplish is of considerable more importance than what is accomplished by the cells, not acting thus as aerial terminals, which convey the energy to them.

Thus if Jupiter is in Aries, such vibratory rates of the Aries frequency as are contacted will have an influence over the life predominantly such as is indicated by the prominence and aspects of Jupiter. Only to a less extent will the influence be that indicated by the aspects of the planet Mars, if that planet is located in some other house of the birth chart.

With this information at our disposal it is no difficult matter to determine quite definitely how close association with anything the astrological rulership of which is known will affect a given individual. If the object is under the direct rule of a planet, the stellar cells which its vibrations will reach in greatest volume are those mapped in the birth chart by the planet.

This planet is located in a certain house of the birth chart, mapping a compartment of the astral body. It will, therefore, be a dynamic stellar structure of this compartment which receives the major portion of this additional energy. And as the thought cells of this whole compartment have had their origin in impulses, feelings, and other mental activities relating to one department, the result of their increased activity will attract events into the life relating to this department. That is, events will be attracted which are ruled by the house of the birth chart containing the planet.

To a minor degree, through the activity gained by the sympathetic response of the stellar cells there mapped, events will also be attracted ruled by any house the cusp of which is ruled by this planet.

If the object is ruled by a zodiacal sign, and thus only indirectly under the rule of a planet, the stellar cells which its vibrations reach more directly are those of the compartment mapped by that zodiacal sign. The major influence, therefore, will relate to the department of life ruled by the house of the birth chart so indicated.

Only in a less degree, because the planetary aerial picks up some of the energy of the vibration of the sign it rules, will energy reach the compartment of the astral body mapped by the planet ruling the sign, and thus have some influence toward attracting events relating to it.

But when there is a planet in the sign ruling the object with which there is association, the type of energy of this planet and its harmony or discord are more important than are those of the planet ruling the sign and elsewhere located.

Therefore, in judging the effect of the character vibrations or thought vibrations ruled by a planet, look chiefly to the house position and aspects of the planet. But in judging the effect of the character vibrations or thought vibrations ruled by a zodiacal sign, look chiefly to the house position of the sign, and to any planet in the sign. If there is no planet in the sign, look chiefly to the house position of the sign in reference to the department of life affected, but to the aspects of the planet ruling the sign to determine the harmony or discord thus accentuated.

Character Vibrations

The kind of business and type of person ruled by each planet and sign are given in Chapter 5 (Serial Lesson 107). The part of the country, climate, part of city and part of home ruled by each sign are given in Chapter 5 (Serial Lesson 90), Course VIII, Horary Astrology. And in Course VI, Sacred Tarot, the herbs and flowers, stones, branch of science and human function ruled by each sign are set forth in connection with the corresponding Major Arcanum of the tarot. Here, therefore, only the briefest mention will be made of important associations ruled by each sign and planet.

Signs

ARIES—Number 13. Letter M. Color, light red. Tone, high C. Talismanic gem, amethyst.

TAURUS—Number 14. Letter N. Color, dark yellow. Tone, low E. Talismanic gem, agate.

GEMINI—Number 17. Letter F, Ph, P. Color, light violet. Tone, high B. Talismanic gem, beryl.

CANCER—Number 18. Letter Sh, Ts, Tz. Color, light green. Tone, high F. Talismanic gem, emerald.

LEO—Number 19. Letter Q. Color, light orange. Tone, high D. Talismanic gem, ruby.

VIRGO—Number 2. Letter B. Color, dark violet. Tone, low B. Talismanic gem, jasper.

LIBRA—Number 3. Letter G. Color, light yellow. Tone, high E. Talismanic gem, diamond.

SCORPIO—Number 4. Letter D. Color, dark red. Tone, low C. Talismanic gem, topaz.

SAGITTARIUS—Number 7. Letter Z. Color, light purple. Tone, high A. Talismanic gem, red garnet.

CAPRICORN—Number 8. Letter H, Ch. Color, dark blue. Tone, low G. Talismanic gem, onyx.

AQUARIUS—Number 9. Letter Th. Color, sky blue. Tone, high G. Talismanic gem, blue sapphire.

PISCES—Number 12. Letter L. Color, dark purple. Tone, low A. Talismanic gem, peridot.

Planets

SUN—Number 21. Letter S. Color, orange. Tone, D. Metal, gold. Flower, helianthus and gaillardia.

MOON—Number 20. Letter R. Color, green. Tone, F. Metal, silver. Flower, lily.

MERCURY—Number 1. Letter A. Color, violet. Tone, B. Metal, quicksilver, Flower, jasmine and honeysuckle.

VENUS—Number 6. Letter U, V, W. Color, yellow. Tone, E. Metal, copper. Flower, rose.

MARS—Number 16. Letter 0. Color, red. Tone, C. Metal, iron. Flower, hollyhock.

JUPITER—Number 5. Letter E. Color, purple. Tone, A. Metal, tin. Flower, dahlia.

SATURN—Number 15. Letter X. Color, blue. Tone, G. Metal, lead. Flower, statice.

URANUS—Number 10. Letter I, J, Y. Color, dazzling white. Tone, astral chimes. Metal, uranium. Flower, clover and oxalis.

NEPTUNE—Number 11. Letter C, K. Color, changing iridescence. Tone, music of the spheres. Element, neptunium. Flower, arctotis.

PLUTO—Number 22 or 0. Letter T. Color, ultraviolet and infrared. Tone, spirit choir. Element, plutonium. Flower, pitcher plant.

What is even of greater importance than to know that association with a particular thing will tend to attract events relative to a certain department of life, as signified by the house position of the sign or planet ruling the thing, is to know whether, and in what way, events so attracted will be fortunate or unfortunate.

This, as I have pointed out, depends upon whether the stellar cells to which the new supply of energy is added through such association, are harmonious or discordant in their activity.

It is quite correct to say that stellar cells or stellar structures in the astral body mapped by planets receiving discordant aspects are discordant in their activity, and that those mapped by planets receiving harmonious aspects are harmonious and tend to attract fortunate events. But in leaving the matter thus we are all too apt to overlook why the thought cells of one person attract fortunate events and the thought cells of another attract unfortunate events when brought in contact with the same associations.

The dynamic stellar structures mapped in the astral body by the planets in the birth chart are composed of stellar cells which are definite thought compounds, the thought elements of which have been united under conditions that give them a harmonious or discordant quality, or feeling. Both the intensity and the kind of feeling, which is present at the time two thoughts or impulses are brought together, influence the manner in which the thought elements unite in a compound.

It is not due to the aspects of the planets that the thought cells in the astral body act harmoniously or discordantly, but due to the circumstances with which the thought elements embraced within them were brought together. The strongest combinations of thoughts within the astral body, the chief ingredient in one region being mapped by one planet and the chief ingredient in another region being mapped by another planet, are connected by a line, or aerial, through the astral body. It is this line, which indicates how the thoughts at each end have united and formed compounds with a less volume of the thoughts at the other end, which is mapped by an aspect in the birth chart.

The aspect is there because the thoughts at each end are in such relation to each other as the aspect indicates. But as these stellar cells and dynamic stellar structures so mapped are thought formed, they may also be thought changed. And when so altered by an intelligent application of the same principles under which they originally were formed, their activities stimulated by new energy from objects, thoughts, or planets will be according to this new relation, and not according to the aspect mapped in the birth chart. The birth-chart aspect only maps their composition at birth, and not such as is later acquired.

An indication of the circumstances under which each of the ten types of thought compounds is formed, therefore, is valuable both in determining what type of harmony or discord will be attracted into the life through association with a particular object, and in setting about to change the trend of fortune in any department of life mapped by a house of the birth chart, the stellar cells of which are shown by planetary aspects to be discordant.

Aspects

CONJUNCTION—This aspect indicates that the thought elements ruled by the planets so joined have had a long and close association, and that the persistent thinking or feeling along the lines indicated has given great volume and energy to the thought compound there located. In this repeated association of mental factors there has been no intense pleasure or intense pain. Such harmony or discord as is indicated belongs to the essential qualities of the thought families so united rather than to the circumstances of their union. A dynamic stellar structure mapped by such an aspect, because of the volume of energy it contains, tends to bring the things ruled by both planets into prominence. Hence it is called a PROMINENCE compound.

SEMISEXTILE—When thought elements of any two families are united by a steady feeling of mild pleasure they form a compound such as is mapped by the semisextile. Such a union of thought elements in a dynamic stellar structure tends to attract conditions offering many small advantages for further growth. It is, therefore, called a GROWTH compound.

SEXTILE—The things thought about, as indicated by one planet, when brought into association with the things thought about as indicated by another planet, under conditions which uniformly give rise to a feeling of pleasure, unite in a thought compound such as is mapped by a sextile aspect. A dynamic stellar structure formed of such harmoniously blended thought elements tends to attract opportunities. Hence it is termed an OPPORTUNITY compound.

SQUARE—This aspect indicates that two types of desires have been present at the same time which were incompatible one with the other. As a result of the obstacles each desire placed in the way of realizing the other, violent discord was experienced. And because the dynamic stellar structure so built tends to attract additional obstacles, it is called an OBSTACLE compound.

TRINE—Things thought about in mutual association with prolonged and enthusiastic pleasure bring a union of corresponding thought elements into the most harmonious of all types of stellar cells. A dynamic stellar structure composed of such cells, because it tends to attract what is commonly called luck, is known as a LUCK compound.

INCONJUNCT—When endeavors, or objects, are brought together in the mind in association with ideas of development, but with no pronounced feeling of pleasure or annoyance, they unite in a compound which is neither markedly harmonious nor discordant. A dynamic stellar structure composed of thought cells so formed tends to attract expansive conditions into the life, and thus is known as an EXPANSION compound.

SEMISQUARE—Irritations, the smaller abrasions of life, and the numerous little anxieties, when they bring together and unite the thoughts about definite types of activities, enter into a compound which is chronically discordant and annoying. A dynamic stellar structure formed in this manner tends persistently to attract friction with others and irritating circumstances, and is called a FRICTION compound.

OPPOSITION—When the desires pull simultaneously in opposite directions, causing a decided feeling of distress because if one course of action is followed another desired course of action must be relinquished, a most energetic compound is formed of the thought elements so united. Because the dynamic stellar structure formed in this manner tends to force asunder those things in the life which are associated with it, it is called a SEPARATION compound.

SESQUISQUARE—Thoughts about things which at one time were pleasurable but later became painful, the reaction being accompanied by a high degree of distaste, tend to enter into a thought union which is disruptive, and which operates to break up, at intervals, the previously existing condition. A dynamic stellar structure thus formed, because agitation is the common mental state when the break up is either contemplated or takes place, is called an AGITATION compound.

PARALLEL—This aspect indicates that the thought elements ruled by the planets have had a long association of rather indefinite quality in which neither pleasure nor pain was pronounced, but of sufficient volume to build, although in a somewhat loose manner, quite a powerful stellar structure. The dynamic stellar structure so formed, because it gives intensity to the power of attracting the things ruled by the two planets, is known as an INTENSITY compound.

GRAND TRINE—When three planets are located in a chart so as to form a complete equilateral triangle, each planet being within orb of a trine to both the others, it is called a Grand Trine. Our research department has conducted a statistical analysis of such Grand Trines in connection with those who have made money, attained honor and attracted other types of success. Because thoughts from three distinct departments of life are harmoniously associated, as indicated by the analyses mentioned the Grand Trine proves to be the most fortunate configuration that can occur. And in so far as the person can live his life in association with the things so indicated will he attract unusual good fortune.

GRAND SQUARE—When four planets in a chart are so located that they form a complete cross, all four arms of which are occupied by a planet, each planet being within orb of a square aspect to its neighbors, and in opposition to the one across the zodiac, it is called a Grand Square. Our research department, through statistical analysis, has found such a Grand Square to be the most unfortunate configuration that can occur in a chart. In the thousands of birth charts with progressed aspects of people suffering from the one-hundred-sixty different diseases considered in Course XVI, Stellar Healing, we found that when there was a Grand Square in the chart the disease almost invariably was indicated by the planets involved in it.

Already, in preceding lessons, it has been shown that the abilities, temperament, disposition, business qualifications and attraction for money which any individual possesses, and which are mapped in the birth chart, are due to the thought cells which have been built by experiences of parallel significance into his astral body. And now that we also know the manner in which thoughts about different things unite to form definite compounds which build up with the stellar cells so formed the dynamic stellar structures mapped by the planets, we are in a position to extend the principle involved to all other departments of life, including friends, enemies, studies, travels and associations.

Instead of considering astrology as the writing of the hand of inevitable fate, if this grand science is used according to its true function, as the Golden Key to unlock the cause of conditions and reveal the processes of nature, it becomes a great boon to mankind. And thus applied in natal astrology, it indicates why—through the thought organization of the astral body, and the receiving of new energy by the stellar cells in a given compartment of the astral body at a specified time—a life has qualities, attracts the conditions, and on given dates undergoes the fortune or misfortune it does.

And in addition, because all are due to the thought composition of the finer form, it shows just how to go about it, through altering the thought composition of the astral body and supplying additional energy to the more fortunate thought groups, to make the life and fortune more as desired. When intelligently and persistently applied, as proved by the letters we receive from students who do this very thing, these methods bring the desired results.

Friends

Because the stellar cells in the compartment of the astral body mapped by the 11th house of the birth chart have been acquired through thoughts and impressions relating to friendship, both the kind of friends attracted, and the type of influence they have in the life, are to be judged from this house.

As the most active thought cells within the astral body are those mapped by the planets, and as each planet maps thought cells which belong to a certain family as they have entered into the composition of a dynamic stellar structure, the location of a planet in a house of the birth chart indicates the type of conditions attracted to this department of life.

If Neptune is in the 11th house, as in the charts of Wm. Jennings Bryan, Sir Arthur Conan Doyle (pages -) and David Belasco, it signifies that the most influential friends in the life will be idealists, psychics and mediums, or people of dramatic talent; because the stellar cells in the friendship compartment of these notables’ lives have been built chiefly of the thought elements of the same family to which the people so attracted belong.

In the birth chart of Professor Nicholas Murray Butler, with the Moon in the 11th, the stellar cells in this compartment of his life have had their origin in contacts with the widest variety of people. Consequently he attracts to him, as friends, those from all walks of life. But Professor A. Van der Nailen (pages -), also with honor in college work, has Mars and Uranus in the house of friends. He, therefore, attracted to him occult students and engineers, eccentric characters and soldiers, because the stellar cells that had been built into this compartment of his astral body were of the same thought family as these people.

When the 11th house of the birth chart is unoccupied by a planet, because the more active thought cells are elsewhere located in the astral body, the influence of close friends, either for fortune or misfortune, is much less than when one or more planets are so located. Such a chart, for instance, is that of David Lloyd George (pages -).

Such influence as friends do have, however, must be determined, not merely by the planets in the 11th, or by the ruler of the cusp of the 11th, but by also taking into consideration the aspects of these planets. Henry Ford (pages -), with Jupiter well aspected in the 11th, benefited greatly by influential friends. He was a close friend of John Burroughs, the writer, as indicated by the sextile of Jupiter to a planet in the 9th, was a close friend of Harvey Firestone and George Eastman, manufacturers, as indicated by the sextile of Jupiter to Mars, and was a close friend of Thomas A. Edison, the inventor, as revealed by Jupiter trine Uranus.

But that fine old gentleman, A. Van der Nailen, with Mars conjunction Uranus in the 11th, suffered persecution from his former friends when he departed from materialism and embraced occult doctrines. And the occult friends and their influence in his life estranged him from his children, as indicated by Mars and Uranus opposition Saturn in the 5th, and they were a severe affliction to him personally, as indicated by the square of Mars and Uranus to the Sun in his 1st.

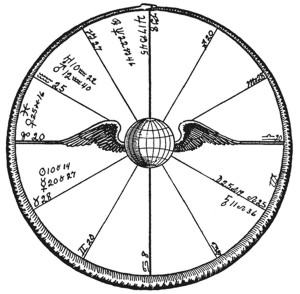Professor A. Van der Nailen May 1, 1830, 8:00 A.M., 5E45; 51N. Internationally known (Jupiter in 10th, trine Sun and Mercury in 1st) physicist. Author (Mercury, ruler of 3rd, trine Jupiter, ruler of 9th) of In the Sanctuary, On the Heights of the Himalayas, and other mystical (Neptune in 10th, trine Mercury) novels. He attracted occult (Uranus) friends, and engineer (Mars) friends. His interest in occultism brought vicious criticism from his engineering friends, and alienated him from his children (Saturn in 5th, opposition Uranus in 11th). He lived, as indicated by Sun in an angle, square Mars and trine Jupiter, almost one hundred years.

Hopes

Not only the impulses and thoughts relating to physical friends, but also to those mental friends and almost constant companions which we call hopes, are embraced within the compartment of the astral body mapped by the 11th house. Not merely the kind of friends, therefore, but the kind of hopes, are indicated by any planet in the 11th, and to a less degree by the planet ruling the cusp of the 11th.

The two great hopes of Abraham Lincoln (pages and ) were to win the war, as indicated by Mars in the 11th trine Sun and square Moon, and eventually to free the slaves, as indicated by the freedom planet, Uranus, in the 11th, trine Mercury. And, although at great cost, for Mars gains its ends only through strife, the trines of these planets enabled him to realize these hopes.

Sir Arthur Conan Doyle (pages -), as indicated by Neptune in the 11th, hoped to convert the world to spiritualism. He toured the globe in the endeavor, and wrote copiously, these activities being indicated by the Moon in the 9th, sextile Neptune. His influence in this direction was probably greater than that of any other man; but, as indicated by Neptune square Jupiter in the 1st, the obstacles encountered were terrific, and his hopes were only partially realized.

Wm. Jennings Bryan hoped for a new ratio between gold and silver in coinage, as indicated by Mercury in the 11th, square Jupiter in the house of money. This, he did not get. He hoped for many socialistic reforms, as indicated by Neptune in the 11th, and hoped to become President of the United States, as indicated by the Sun in the 11th. He was able to exert a powerful influence, but he never became President; and his hope of success as Secretary of State, to which office he had been appointed, was blighted, as indicated by Neptune and the Sun in the 11th square Mars in the house of war. His conscientious objections were such an obstacle that when the U. S. entered the war he resigned this one important position which he held.

Disappointments

The thoughts, feelings and emotions relating to sorrows, restrictions and disappointments are built into the stellar structure mapped by the 12th house. An individual may realize important hopes in one direction and have equally keen disappointments relating to other things.

Mr. Bryan had three planets in his 12th house. His disappointments were no less outstanding than his realizations. His sorrow when the U. S. entered the World War knew no bounds; for Pluto, the planet of universal welfare, in the 12th was for peace at any price.

Abraham Lincoln’s (pages and ) early love for Ann Rutledge, instead of resulting in marriage—Mercury square planets in the 12th—was defeated by her death—Mars ruler of 5th, square Moon, ruler of the 8th. Saturn and Neptune in the 12th made of him a man of many sorrows.

People with many planets in the 12th may attain as great success as those with no planets in this house; but because the thought cells relating to disappointments are so energetic they attract to themselves many sorrows. Quite frequently these disappointments are due to their own attitude or actions; although others may be the result of the actions of secret enemies, or due to circumstances of which they have no knowledge.

These actions which bring disappointments may be due to inability to appreciate the effect of a certain course of conduct, or it may be due to premeditated conduct in spite of recognized consequences. Wm. J. Bryan was quite aware that his radical views would bring him difficulties (Uranus in 12th, conjunction Asc.), and he resigned as Secretary of State as a conscientious objector to war.

Arthur Conan Doyle (pages -) well realized that he would be persecuted for espousing spiritualism, but the ruler of his Asc. was in the 12th, conjunction the universal welfare planet, Pluto; therefore, he went ahead with what he considered his duty, in spite of its effect upon him personally or upon his reputation (ruler of 10th in 12th).

Studies, Writing, Publishing, Brethren

The thoughts, impulses and feelings relative to physical brethren and to those mental brethren which are the studies are chiefly retained in the thought compounds of the compartment of the astral body mapped by the third house.

In general, therefore, the type of brothers and sisters an individual has, and more particularly the amount of fortune or misfortune of their influence in the life, may be determined by the planets and their aspects relating to the 3rd house. Furthermore, at those times when their influence will be marked in the life there will be found a temporary stellar aerial leading to this compartment as mapped by a major-progressed aspect within one degree of perfect to the ruler of the 3rd house. For instance, the reference book, When and What Events Will Happen, shows by detailed analysis that when brother or sister dies there is always a major-progressed aspect within one degree of perfect both to the ruler of the 3rd and to the ruler of the 8th.

The private studies and the writing that results from them are also to be judged from the 3rd house. Thus Saturn here gives depth of thought; although the mind unfolds more slowly. Mars in the 3rd tends to an early and energetic development of the mind. Uranus gives originality in thought and studies, and Neptune supplies imagination. A number of planets in the 3rd house increases the tendency to study. But of even greater importance in conferring ability to study, write and travel are the prominence and aspects of the three planets, Mercury, Uranus and the Moon.

Discordant aspects to the ruler of the 3rd, or to the three mental planets mentioned, do not impair the power of thought; but they attract unfortunate events according to the inharmony shown.

The public expression of the thoughts, through teaching, lecturing, advertising or the medium of printed books or periodicals is related to the stellar cells contained within the compartment of the astral body mapped by the 9th house. Conan Doyle (pages -), for instance, had the Moon in the 9th, indicating that to the extent they were received his writing would have a universal appeal. The Moon makes some aspect to each of the six planets in his 12th house, the house of crime, mystery and detectives. His fame rests upon his Sherlock Holmes detective stories. Mercury, Uranus and the Moon all are prominent.

A. Van der Nailen (pages -) had no planets in his 9th, but the ruler of the cusp of the 9th is Jupiter. Jupiter is the religious planet, is in conjunction with Neptune, the mystical planet, and both are trine the writing planet, Mercury, in the 1st. His contributions to science were overlooked; but his mystical-religious novels are still widely read. Mercury, Moon and Uranus are all prominent.

Religion

The type of religion an individual embraces must be determined from the chart as a whole, as the prominence of the upper-octave planets indicates a progressive trend. But the influence on the life of the public expression of whatever religious, philosophical, or other beliefs are held may be determined from the 9th house.

If Mars is there the publicly expressed beliefs will bring strife. If Uranus is there the individual will be considered eccentric. If Neptune is there, people will think him visionary in his doctrines. Conan Doyle’s detective novels brought the acclaim of his Moon trine Sun and Uranus; but his deeper thoughts, as indicated by Saturn in the 3rd, in opposition to the Moon, when expressed, brought him opposition, and the obstacles indicated by the Moon square Mercury and Pluto in the 12th.

Secret Enemies and the Influence of Astrals

The more active, as shown by planets in the 12th, the stellar cells are which compose the compartment of the astral body relating to enemies, the more secret enemies will be able to influence the life. But their power to damage must be gauged by the nature of the planets in the 12th and their aspects.

Conan Doyle’s (pages -) chart, because so many planets are in the 12th, attracted many secret enemies. They were of all six types indicated by the six planets there. And as the 12th also indicates the compartment of the finer body where contact is made with astral entities, his contact with the invisible world was wide and varied, and not confined to well-disposed humans who had passed from earth life. But the power of either physical or astral enemies to injure him was limited by the splendid aspects, Venus sextile Jupiter, and Sun trine Moon.

Lloyd George (pages -) had secret enemies of three types, as shown by three planets in his 12th. But Mercury there, trine Uranus, enabled him more frequently to defeat them.

George Bernard Shaw (pages and ) also has three chief types of secret enemies, as indicated by three planets in the 12th. And to a less degree than Doyle, both he and Lloyd George have ability to get to the bottom of things; for the 12th not only has to do with secret enemies, hospitals, places of detention and underhanded plots, but also relates to crime detection. Shaw, similar to Doyle and Bryan, has both the exposé planet, Uranus, and the universal welfare planet, Pluto, in the 12th. He dotes on turning up and exposing the methods employed by the wealthy in exploiting the downtrodden.

Open Enemies

The thoughts, feelings and mental attitudes toward those who are met publicly are retained in the compartment of the astral body mapped by the 7th house. Therefore, because these determine the conditions surrounding open contact with others, not only the public enemies, but the general reception from the public, and the circumstances surrounding contacts with the public, are to be judged from the 7th house.

The writer of these lessons has Jupiter in the 7th, and aside from writing has for many years appeared before the public in person as a lecturer on THE RELIGION OF THE STARS, and as a naturalist, having been associated with clubs devoted to nature study also for a long time, just now being president of The Nature Club of Southern California. The only public enemies he has ever made, in so far as he is aware, have been due to his religious views.

Jupiter is the ruler of the 7th in Conan Doyle’s (pages -) chart, and is conjunction with Mars in the 12th and square Neptune in the 11th. His open enemies, as well as those more secret, were also due to his religious opinions.

Lloyd George (pages -), with Saturn in the 7th, contacted his public in the serious statesmanship of handling practical affairs. He has had powerful public enemies among the conservatives indicated by Saturn, and also among the socialists, as indicated by Neptune in opposition to Saturn. As this is written the socialistic opposition thus shown, headed by Ramsey MacDonald, has forced him into comparative obscurity. But during the World War, Saturn in the house of war, trine Venus and Mercury, enabled him as head of the British Government, to bring about the defeat of her opponents.

Wm. Jennings Bryan, with Mars in the 7th, had open enemies of a different kind. His peace at any price caused army men to hate him, and his violent assaults on intoxicants, also ruled by Mars, made the liquor interests furious. War caused him to resign the most important office he ever held, and he was constantly fighting for the under dog. It was this willingness to fight for the interests of the common people, as indicated by Mars in the 7th, sextile Moon in the 10th, that not only won him public enemies, but which gave him the great popularity that he deservedly possessed.

Journeys

The experiences with long journeys, and the thoughts and feelings so engendered, are retained in the stellar cells of the compartment mapped by the 9th house; and those derived from short journeys are a part of the composition of the stellar structure mapped by the compartment of the astral body mapped by the 3rd house.

The more activity these stellar cells, and the stellar structures they form possess, the more strongly are journeys attracted into the life. But, as accentuating this influence, the three travel plants, Mercury, Moon and Uranus also must be considered. Their stellar structures, to the extent these planets are prominent and have powerful aspects, tend toward not merely mental activity, but also toward change and travel.

But the circumstances surrounding the journeys are to be judged from the 9th house for long journeys and from the 3rd house for short journeys. In compiling the information on journeys in the reference book, When and What Events Will Happen in which 100 long journeys and 100 short journeys are analyzed, it was evident that progressed aspects to the travel planets made travel more certain, but that people do not take journeys under progressed aspects to these or other planets unless at the same time, in the case of long journeys there is a progressed aspect to the ruler of the 9th, and in the case of a short journey there is a progressed aspect to the ruler of the 3rd.

What fortune or misfortune accompanies such journeys, and the general nature of them, must also be judged from the planet ruling the house in the birth chart. If Mars is in the 3rd, short journeys will be accompanied by strife or danger. If Uranus is chief ruler of the 3rd, short journeys will be taken abruptly and with little preparation. If Saturn is chief ruler of the 9th, long journeys will be tiresome and laborious. If Neptune is in the 9th, sea journeys are indicated, or at least the long journeys will have a romantic setting.

Birth Charts

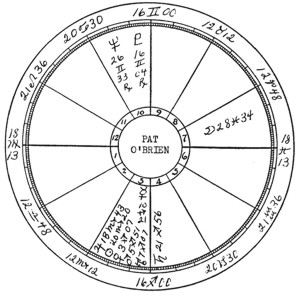
Pat O’Brien November 11, 1899, 1:30 A.M. CST Milwaukee, Wisconsin, 43N02; 87W55. Data from Sabian Symbols Friends: see page . As no planet appears in the 11th house, the ruler of the 11th cusp, the Moon, describes his friends. The Moon does square Saturn and Neptune, but it has six trines: with the sun, Mercury, Venus, Mars, Jupiter and Uranus. One of the best loved actors in Hollywood, he is extremely popular with a host of friends. Marriage: see chapter 7 (Serial Lesson 109), "Love, Marriage and Partnership." In a business notorious for divorces, he holds a record. January 31, 1961 he and his wife, Eloise, celebrated their 30th wedding anniversary.

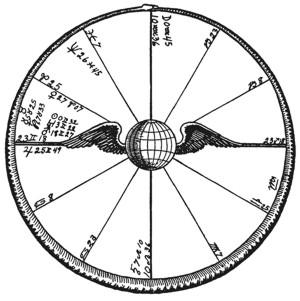
Sir Arthur Conan Doyle May 22, 1859, 4:55 A.M.. 3W; 56N 1885, married: sun conjunction Jupiter r. 1885, started practice of medicine: sun conjunction Jupiter r. 1887, first publication: Venus conjunction Sun r and sextile Moon r. 1891, Sherlock Holmes: Sun conjunction Mercury p, Venus conjunction Uranus p. 1902 knighted: Sun semisextile Saturn p, Jupiter semisextile Uranus p. 1907, married: Venus conjunction Jupiter r. 1917, most influential champion of spiritualism: Sun trine Neptune r.

To purchase the print book Delineating the Horoscope click here