| |
|
|
| |
 |
|
| |
 |
|
| |
 |
|
| |
 |
|

Serial Lesson 222
From Course XXI, Personal Alchemy, Chapter 7
Original Copyright 1949, Elbert Benjamine (a.k.a. C. C. Zain)
Copyright 2012, The Church of Light
Subheadings: Calcium Supply More Vitamin B-1 Stabilize With More Calcium To Benefit, the Calcium Must Be Assimilated Vitamin D Must Be Present to Handle the Calcium Use Jupiter Thoughts to Neutralize Discordant Mercury or Uranus Thought-Cell Activity Influence of the Foods Upon the Disposition
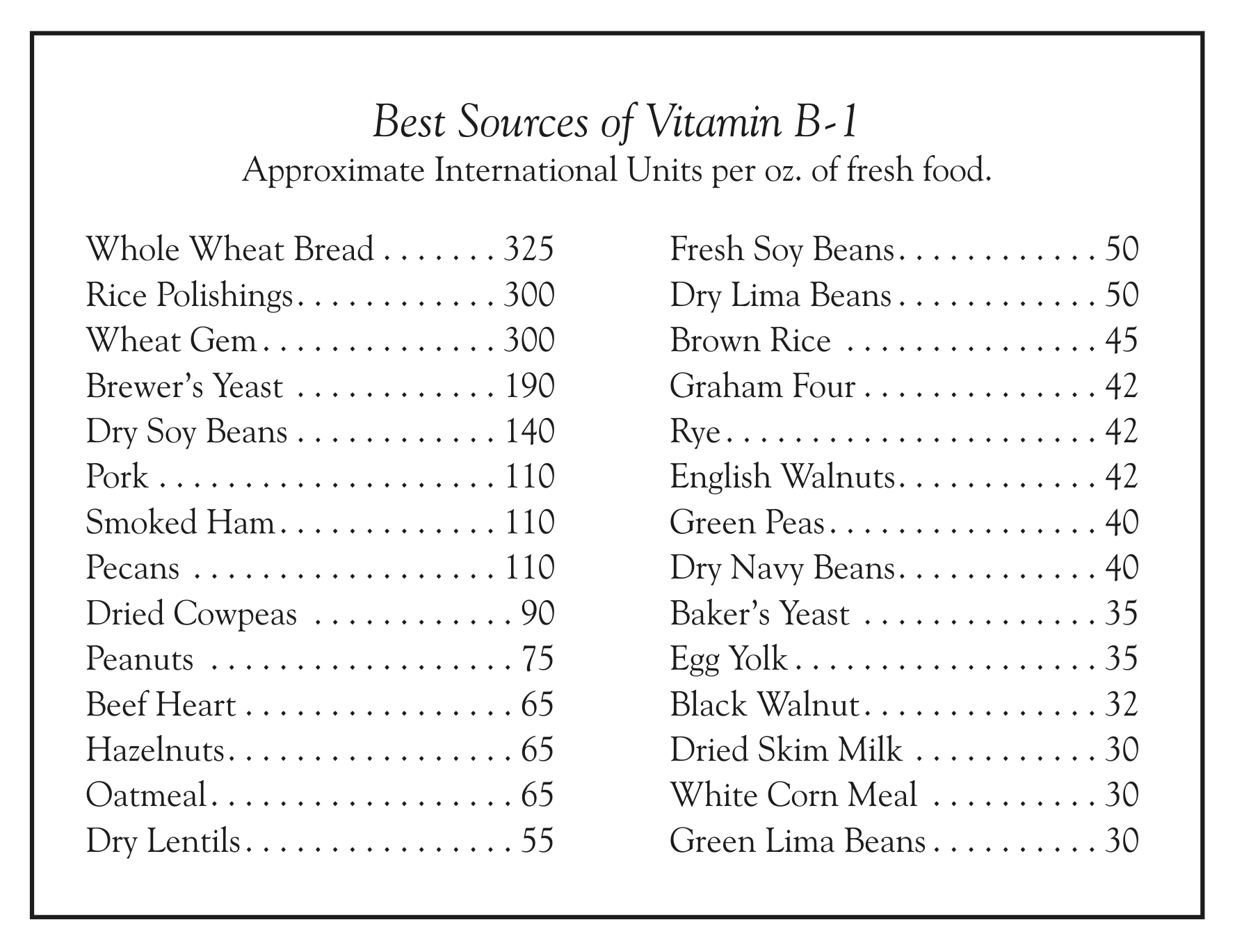
Charts: Best Sources Vitamin B1 Chart Best Sources Calcium Chart
Chapter 7
What to Eat When Mercury or Uranus is Afflicted

MAN is a two-plane organism whose outer plane body is composed of physical cells and structures and whose inner-plane body is composed of thought cells and thought structures. He is influenced about equally by his outer-plane environment and by his inner-plane environment. Heat and cold, rain and wind, food and people and inanimate objects affect his physical body; and his states of consciousness coincident with such physical responses in turn add energy to and somewhat change the thought-cell organization of his finer form.
A great deal of carefully checked observation indicates that the inner-plane weather mapped by progressed aspects affects him as much, and probably more, than the outer-plane weather. The thoughts of people and of inner-plane entities, and the inner-plane radiations from objects also add their energies to certain groups of thought cells within his finer form, giving them greater activity than usual, and thus enable them through his electromagnetism profoundly to influence his physical body.
One of the means through which the chemistry of the physical body is so quickly altered by such thought-cell activity is the system of endocrine glands, ruled by the Sun. These are the glands of internal secretion. They manufacture complex compounds called hormones from materials, chiefly the proteins, which they get from the blood and lymph. Each endocrine gland manufactures its own hormone or hormones, which differs in chemistry and function from the hormones manufactured by the other glands. These hormones are not emptied into a duct which carries them to the region to be influenced, but instead are liberated directly into the blood stream. That the hormones may thus find easy access to the blood stream, and through the blood stream to the region to be affected, the endocrine glands usually have a rich supply of blood vessels.
Now the activity of any endocrine gland may be stimulated by a thought or emotion, by the thought-cell activity within the soul accelerated by the energy of a progressed planetary aspect, or by the hormones of other endocrine glands. Their ready response to conscious thought, or to unconscious thought-cell activity inaugurated by a progressed planetary aspect, is accomplished by nerves which carry electrical impulses to the glands. Yet it has only been since 1936 that nerve currents have been recognized by science to be electrical, and only since 1922 that science knew anything about the control the endocrines exert over the body.
When, influenced by thought, emotion or thought-cell activity the hormone of a gland enters the blood, it is carried along in the general circulation and distributed to all parts of the body. All the cells and tissues are bathed in the fluid carrying it, and some cells and organs and other glands respond to it in a marked way, even though distantly located in the body.
Among other things these glands—each of which is delicately responsive to the thought-cell activity inaugurated by the energies of one or more specific planet—determine the size, shape and texture of the body; make for intelligence or its lack; give courage or cowardice; imbue with ambition or saturate with laziness; prompt to moral actions or to those immoral; and in general force the given outlook upon life. And they determine the chemistry of the body at a given time, and therefore just what foods are needed to keep or restore health.
I do not wish to be understood as implying that progressed aspects alone are instrumental in accelerating specific glandular secretions. Thought-cell activity such as is ruled by any planet can be increased by appropriate conscious thinking. Conscious thinking is boundary-line thinking, imparting some of its energy to corresponding thought cells within the soul, and some of its energy more directly by means of nerve currents to the glands. Also heat or cold, and the foods taken into the system, act from the outer plane to increase or depress glandular activities. What I do wish to state is that, regardless of the cause of glandular activity, the hormones they secrete chiefly determine the chemistry of the body and therefore what it needs at a given time in the way of food.
Not only so, but because each endocrine gland is so responsive to thought-cell activity of the type ruled by specific planets, its tendency to be influenced from normal at times which can be predetermined is mapped by the progressed aspects of the planets which have energy of the type to which it responds. And because the prominence and aspects of the planets in the birth chart map the relative amount of thought-cell activity of the various kinds at birth, the general predisposition of the individual to over or underactivity of certain glands may be ascertained from the chart of birth.
Not only do some of the endocrine glands secrete more than one hormone, or chemical messenger, but several of them respond with almost equal alacrity to types of thought-cell activity ruled by more than one planet. Not all of the hormones of these glands have as yet been isolated, and the front pituitary which a few years ago was considered to secrete only one hormone, is now known to manufacture not less than twelve; even as vitamin B also in the meantime has been found to comprise many vitamins, twelve of which have now been discovered, the whole of which are now known as vitamin B complex Long and close observation by The Church of Light Astrological Research Department relative to the effect of progressed aspects and birth chart prominence on hormone activity has established that each of the planets through birth chart prominence and by progressed aspect finds ready response from the endocrine glands as follows:
SUN: influences two of the hormones of the front pituitary gland, one of which stimulates the thyroid gland and otherwise contributes to the transformation of energy necessary for sustained effort; and the other stimulates the adrenal cortex and thus with that gland determines the presence of courage.
And it influences the secretion of thyroxin, the hormone of energy production. These three hormones respond either to thought-cell activity stimulated by progressed aspects involving the Sun, or to conscious thinking of the Power type.
MOON: influences the two hormones of the back pituitary, the thymus hormone, and the hormones of the alimentary tract. One back pituitary hormone regulates woman’s periodic functions. Pituitrin, the other back pituitary hormone, causes water to be retained in the body and the contraction of all the arteries except those of the kidneys. It causes the contraction of the plain muscles of the bowels, the bladder, the womb and other organs. It is sometimes used in childbirth to contract the womb. It also has something to do with the metabolism of the carbohydrates. Its deficiency leads to obesity. The thymus hormone tends to retard attaining maturity. These hormones respond either to thought-cell activity stimulated by progressed aspects involving the Moon, or to conscious thinking of the Domestic type.
MERCURY: influences the hormone of the parathyroid glands and one of the hormones of the front pituitary. Parathyrin, the hormone of the parathyroid glands, controls the calcium metabolism of the body, and in combination with other hormones ruled by Mercury, Uranus, Neptune and Pluto, controls the type of electrification. The front pituitary hormone which responds to Mercury influences cerebral activity. These two hormones respond to thought-cell activity stimulated by progressed aspects involving Mercury, or to conscious thinking of the Intellectual type.
VENUS: influences the hormone of the thyroid gland and the hormones of the gonad glands. Testosterone is the male sex hormone of the testes. Alphaestradoil has been found to be the active principle of estrone, the female hormone of the ovaries. It is now commonly referred to as the estrogenic hormone. These gonad hormones contribute to virility and rejuvenation. The corpus leuteum hormone, progestin, the hormone of pregnancy, also responds to Venus. The thyroid secretion, thyroxin, is the hormone of energy production. These hormones respond either to thought-cell activity stimulated by progressed aspects involving Venus, or to conscious thinking of the Social type.
MARS: influences the hormones of the adrenal glands, and the hormones of the gonad glands. Testosterone, the male sex hormone, secreted by the testes, has been given great publicity as a generator of male virility and as a rejuvenator of the whole body. The adrenal glands secrete two hormones. Adrenaline, secreted by the adrenal medulla, is the hormone of emergency energy. Cortin, secreted by the adrenal cortex, is the hormone of courage. Both adrenal hormones neutralize toxicity of the blood and are the chief chemicals used by the body to fight infection. These sex hormones and adrenal hormones respond either to thought-cell activity stimulated by progressed aspects involving Mars, or to conscious thinking of the Aggressive type.
JUPITER: influences the hormone of the pancreas, insulin. Sugar and starch can only be used as fuel by the body, or as the kindling necessary to burn fat, when insulin is present. The liver is the central banking system of the body where reserve fuel is stored in the form of animal starch, or glycogen. Such storing depends upon the supply of insulin. This hormone responds either to thought-cell activity stimulated by progressed aspects involving Jupiter, or to conscious thinking of the Religious type.
SATURN: influences one hormone of the front pituitary gland. This hormone governs the growth of the skeleton and supporting tissues. Saturn, equally with Mars also influences one secretion of the adrenal glands, adrenaline, the hormone of the medulla. This is the hormone of emergency energy. These two hormones respond either to thought-cell activity stimulated by progressed aspects involving Saturn, or to conscious thinking of the Safety type.
URANUS: influences one hormone of the front pituitary—the one related to original thinking—and it influences the secretion of the parathyroid glands. Parathyrin, the hormone of these glands, controls the calcium metabolism of the body, and in combination with other hormones ruled by Mercury, Uranus, Neptune and Pluto, controls the type of electrification. These Uranus hormones respond either to thought-cell activity stimulated by progressed aspects involving Uranus, or to conscious thinking of the Individualistic type.
NEPTUNE: influences the hormone of the pineal gland, and the hormone of the parathyroid glands. The hormone of the pineal gland prevents precocious maturity, and it neutralizes and depresses the secretion of adrenaline and cortin. Parathyrin, the hormone of the parathyroid glands, controls the calcium metabolism of the body, and in combination with other hormones ruled by Mercury, Uranus, Neptune and Pluto, controls the type of electrification. These Neptune hormones respond either to thought-cell activity stimulated by progressed aspects involving Neptune, or to conscious thinking of the Utopian type.
PLUTO: influences the hormone of the pineal gland, one hormone of the front pituitary—the one related to cooperative effort—the cortin hormone of the adrenal cortex, and the secretion of the parathyroid glands. The hormone of the pineal gland prevents precocious maturity, and it neutralizes and depresses the secretion of adrenaline and cortin. Cortin is the hormone of courage, neutralizes toxicity of the blood, and is one of the chief chemicals used by the body to fight infection. Parathyrin, the hormone of the parathyroid glands, controls the calcium metabolism of the body, and in combination with other hormones ruled by Mercury, Uranus, Neptune and Pluto, controls the type of electrification. These Pluto hormones respond either to thought-cell activity stimulated by progressed aspects involving Pluto, or to conscious thinking of the Universal Welfare type.
Not only do the hormones of the endocrine glands chiefly determine the chemistry of the body at any given time, but through their system of checks and balances it is their function to keep the chemical composition of the body constant within narrow limits. In addition to the central nervous system man possesses an autonomic nervous system, which itself is divided into two sections called the sympathetic nervous system and the parasympathetic nervous system. The action of the parasympathetic nervous system tends to counteract, and affords a check and balance against, the action of the sympathetic nervous system. And in a similar manner certain hormones of the endocrine system afford checks and balances against other hormones which cooperate to produce activities of an opposite character.
Thus does the parathyroid secretion, parathyrin, tend to counteract the action of other hormones and other conditions which tend to irritate or give undue sensitivity to the nerves. This it does chiefly through increasing ability to handle that great stabilizer of bodily chemistry, calcium. Thus also does the secretion of the pineal gland counteract the ability of adrenaline and cortin to overcome the acidity of the blood stream and to fight infection.

Calcium
Calcium, which is ruled by Saturn, constitutes a larger proportion of the body weight than does any other of the mineral elements. Even as Saturn rules those traits which stabilizes the character, and the skeleton which stabilizes the body, so does calcium exercise a stabilizing effect upon the chemistry of the blood stream and nerves. To be more specific, there are a number of mineral salts which play an important part in the physical body, due in great part to their electrical properties. Potassium, sodium. magnesium, iron, copper, manganese and calcium are important for proper nutrition combined as phosphates, carbonates, chlorides, etc. Unless properly controlled the intake of some of these minerals tends to develop chemical imbalances. And it is the special function of calcium to correct such inorganic lack of equilibriums in the body, in whatever direction they may occur. For instance, any unusual condition produced by excesses of sodium or potassium is corrected by an increase of calcium; too much magnesium induces a general state of relaxation, and this may be overcome by additional calcium; and a proper balance between calcium and phosphorus is essential for the proper functioning of nerves and brain.
This regulating the amount of calcium in the blood and the way it functions in the tissues is carried out by four little glands, each about the size of a grain of rice, distributed about the thyroid gland. These are the parathyroid glands. Insufficient of their hormone, called parathyrin, causes the bones to soften, the nails to become brittle, the teeth to fail, and the person to become excessively nervous and excitable. Calcium neutralizes the influence of sodium and other elements in their tendency to irritate the nerves and make them unduly sensitive. Depletion of parathyrin—which responds to the thought-cell activity inaugurated by Mercury, Uranus, Neptune or Pluto—results in inability to handle calcium, resulting in nervousness.
People who are sensitive are those with Mercury, Uranus, Neptune or Pluto thought cells so active that they tend to deplete their supply of parathyrin. Such thought-cell activity tending to parathyrin depletion may be mapped by birth chart or progressed afflictions to one of these four planets, or it may be due to conscious thinking of the type ruled by one of them. Ordinarily, however, the thought-cell activity within the soul is reflected in the trend of the conscious thinking. Frictions or conflicts of any kind within the mind, or over mental activity, tend to disturb the proper action of the parathyroids, and induce a neurotic state. The removal of the parathyroid glands results in a nervous disorder called tetany.
While Mercury, Uranus, Neptune and Pluto thought-cell activity seem equally effective in their influence over the parathyroid secretion, each of these types of thought-cell activity affects also a different endocrine secretion. This, in turn, encourages the corresponding type of thinking—intellectual, original, utopian, universal welfare, according to whether the energy is from Mercury, Uranus, Neptune or Pluto—and has a direct effect upon the frequency of electromagnetic radiations generated in the nervous system.
The cells of the body are miniature batteries which generate electricity and radiate the high-frequency energy of the lightning which fixed the nitrogen that plant life took from the soil. This is in accordance with Einstein’s Law of Equivalence; that the energy of an atom is given out in the same quanta as those received by the atom. And of the cells of the human body, those of the nervous system are best adapted to the production of shortwave radiations, as well as to carrying electricity. But thought-cell activity determines, through the action of the hormones of the endocrine glands, the frequency of the wave lengths radiated at a given time. And this thought-cell activity, in turn, may arise chiefly from the stimulation of factors within the soul by the energies of a progressed aspect, or by a consciously selected mood and trend of thought.
But if the dominant thought-cell activity at the time is of the Mercury type, the electrical energies generated by the nervous system tend to be of the particular frequencies adapted for use in cerebral thinking. This particular range of frequencies is encouraged by the front pituitary hormone which responds to Mercury, in cooperation with parathyrin. Such intellectual effort as that which commonly goes by the name of objective thinking, including problem solving, worry and ordinary fantasy thinking consumes electrical energy which radiates these electromagnetic wavelengths. And when they are called upon excessively it depletes the parathyrin supply, leading to nervous exhaustion, and consuming electrical energies that otherwise would generate the Sun frequencies and contribute to physical vitality.
If the dominant thought-cell activity at the time is of the Uranus type, the electrical energies generated by the nervous system tend to be of the particular frequencies adapted for use in original thinking and in inspirational extrasensory perception. This particular range of frequencies is encouraged by the front pituitary hormone ruled by Uranus, in cooperation with parathyrin. Such intellectual ESP is practiced unconsciously by most writers and inventors, and by many businessmen who, when confronted with a difficult problem, put it from their minds and spend the afternoon on a golf course, confident that before the day is done the proper step to take will pop into their consciousness.
These electromagnetic energies of the Uranus frequencies when generated in excess, not only rob the vitality of the electrical energies needed, but create a high nervous tension which in extreme instances gives rise to uncontrolled muscular twitching, St. Vitus’s dance or paralysis.
If the dominant thought-cell activity at the time is of the Neptune type, the electrical energies generated by the nervous system tend to be of the particular frequencies adapted for use in dramatic work, imagination and feeling extrasensory perception. This particular range of frequencies is encouraged by the pineal hormone influenced by Neptune, in cooperation with parathyrin. It gives a hypersensitivity of the nervous system which tends to make of it and the electrical energies flowing over it, a receiving set for picking up the astral radiations of the person or object which is tuned in on. These wave lengths seem particularly adapted also to permit whatever vibrations are thus picked up to cause their source to be seen, heard, tasted, smelled or felt by objective consciousness. When generated in excess, not only do they rob the vitality and intellect of needed energies, but the individual becomes so sensitive that he suffers acutely merely from the discordant thoughts of people.
If the dominant thought-cell activity at the time is of the Pluto type, the electrical energies generated by the nervous system tend to be of the particular frequencies adapted for cooperative activities and inner-plane work. This particular range of frequencies is encouraged both by the pineal hormone influenced by Pluto and the front pituitary hormone ruled by Pluto, in cooperation with parathyrin. To the extent the pineal hormone is active do the electrical energies seem to work on the negative phase, and to the extent the front pituitary hormone and cortin (also influenced by Pluto) are active do they work on the positive phase. Thus they may be used to pick up energies as a receiving set, or to send messages as a transmitting set, and to do work on the inner plane. When generated in excess they lead to over sensitiveness, and rob the vitality of energy it needs.
The best way of determining the power of a planet is to calculate its astrodynes, as explained in Course XVI, Stellar Healing. This method shows that a planet receiving powerful aspects has much power. But for the statistical analysis of large numbers of charts calculating the astrodynes is too much labor. Therefore, for such volume statistical analysis, on January 1, 1948, we adopted the following rule: Any planet aspecting another planet by zodiacal longitude within one degree of the perfect aspect, or in an angle, or aspecting Sun, Mercury or the Moon is considered prominent. This rule eliminates any non-mathematical opinion on the prominence of a planet. While it may not be as precise as might be desired, it gives uniformity in the statistical analysis of charts.
To the extent a planet is prominent in the chart of birth are the type of thought cells it rules generally active throughout the life. And if at the same time the planet is heavily afflicted, will such activity as they have generally, or temporarily through energy added to the thought cells by a progressed aspect, be of a character unduly to affect the secretion of the hormone or hormones which in particular is influenced by them.
When, therefore, Mercury, Uranus, Neptune or Pluto is of outstanding prominence in the birth chart, or more than one of them, we may by that token expect considerable strain on the parathyroid glands, and if the planet is heavily afflicted the strain will be more pronounced. Birth chart positions, however, chiefly indicate predispositions which only become serious afflictions when there is a progressed aspect involving the planet indicating the predisposition. That is, the thought-cell activity which manifests as discord has only a certain power on the average. But when a progressed aspect forms to the planet mapping it, the thought cells gain a tremendous amount of new energy and become proportionally more active, and influence the things they rule markedly. And if the progressed aspect is discordant, the tendency will be to affect adversely the endocrine secretions which are responsive to the planets involved.
Thus does a progressed aspect involving Mercury, Uranus, Neptune or Pluto tend to develop parathyrin deficiency, and the nerve tension or nerve hypersensitivity which results. Yet if the parathyrin which is present has ample material at hand for stabilizing the nerves and manufacturing healthy nervous tissue, the strain on it will be less because it has so much less work to do; and these same materials also will assist in the production of a normal supply of parathyrin.

Supply More Vitamin B-1
For building healthy nerve tissue vitamin B-1 is essential. And as the necessity to build or repair nervous tissue is greater when Mercury, Uranus, Neptune or Pluto is afflicted, so should the intake of vitamin B-1 then increase. And it should be remembered that if the water in which foods are boiled is thrown away, the vitamin B-1 may be lost. Also that long exposure to heat destroys it.

Stabilize With More Calcium
Phosphorus in ample amounts must be present for bone replacement and for healthy action of brain and nerves. Recent studies of the nervous system of various animals show that as the brain and nervous system become more complex there is an increase in them of compounds of oxygen-poor fats with phosphoric acids. It would seem, then, that even as Saturn rules the calcium in the human system, so phosphorus is ruled by Mercury. Although the idea that phosphorus is a brain food for a time fell into disrepute, late chemical studies verify this conclusion. Brain workers do need foods containing phosphorus, and people need phosphorus when Mercury or Uranus is afflicted.
Yet I emphasize calcium rather than phosphorus because as a rule the foods high in calcium content are also high in phosphorus, and if the individual eats enough of such foods to acquire adequate calcium, he at the same time obtains adequate phosphorus. The bones and teeth, which contain over 99 per cent of the calcium of the body, also contain about 70 per cent of the phosphorus, and there is about two-thirds as much phosphorus in the body as there is calcium.
The phosphorus needed by the body may be obtained from unmilled wheat and oatmeal, Brazil nuts, almonds, beachnuts, beans, lean meat, milk, eggs and cheese. These are all good sources of phosphorus. And, because their presence is so continuously essential, a reserve supply of both calcium and phosphorus is stored in the bones, to be drawn upon as needed, even as a reserve of immediately available fuel in the form of glycogen is stored in the liver.
The bones and nerves must have both calcium and phosphorus, and both are handled by parathyrin. But especial attention must be given calcium because its deficiency is so common and because when there is an affliction of Mercury, Uranus, Neptune or Pluto there is a tendency to inadequate parathyroid secretion, leading not only to lack of calcium-phosphorus balance, but to an increase in the proportion of sodium in the blood and nerves. Such lack of calcium in proportion to sodium quickly affects the nerves and brain.
The effect is to increase the sensitivity of the nerves, to develop high nervous tension, to impair self-control, to speed up and make irregular the mental activity, and to beget the excitability and irritability which are characteristic of neurosis and the tendency to nervous prostration. There is no doubt that effort will enable the individual to increase his self-control, but in spite of any thinking he may do, or any exercise of willpower, his nerves will continue highly sensitive and irritable until they are furnished with sufficient calcium to counteract the chemical attack on them of the excess sodium.
Proper thinking may attract the individual to a calcium supply, but when due to thought-cell activity stimulated by a progressed aspect involving Mercury, Uranus, Neptune or Pluto, reserves of calcium have been drawn from the bones until such supplies are no longer adequate, the only way nervous control can be reestablished is through furnishing them with a better supply of calcium. Thinking alone will not do it; no more than thinking will prevent hydrochloric acid from burning the hand when some of it is accidentally spilled on it.
I am not here attempting to outline a complete diet plan for the individual who is under a progressed affliction involving some planet. I could not do this because not less than a thousand chemical compounds have already been found in the human body, and the diet of the individual should be determined by the proportions in which these compounds exist in his body at the particular time. And this, in turn, is influenced not by one birth chart or progressed aspect alone, but by all of them and by the conditions in his physical environment. By environment I mean not only the available foods but such factors as whether it is winter or summer, and whether he is in the arctic regions or in the tropics.
But I am pointing out that when he is under a progressed affliction involving Mercury, Uranus, Neptune or Pluto, there is special need for vitamin B-1 with which to build healthy nerve tissue, and for calcium with which to facilitate the neutralizing of excess sodium and other elements in the blood stream. And the most effective way to obtain either vitamin B-1 or calcium is to eat foods which abundantly contain it. The tables here published show the best sources of both. White flour and polished rice have been deprived of much of their calcium, and cereals in general, oatmeal in particular, tend to prevent the absorption of calcium by the system.

To Benefit, the Calcium Must Be Assimilated
The calcium in some foods is easily assimilated, while in others is only partly assimilated. For instance, spinach contains .078 per cent calcium, and thus is richer in this mineral than peanuts, brown rice, eggs, etc. But the system seems to be unable to assimilate calcium from spinach. Not only so, but spinach eaten at the same meal with other calcium containing foods decrease the amount of calcium assimilated from them.
Cereals taken with a meal tend to prevent calcium assimilation; but if they are irradiated with ultraviolet light, this effect is not present. Nor do they hinder calcium assimilation when at the same meal lettuce, liver or eggs are eaten.
On the other hand, it is found that an acid condition of the intestinal tract produced by drinking orange juice gives remarkable ability to assimilate the calcium foods. And in addition, orange juice before the commencement of a meal tends to decrease and overcome the acidity of the body; for the fruit acid is burned to give a residue of alkaline carbonates and bicarbonates. The juice of other citrus fruits in like manner tends to increase the ability of the intestines to handle calcium. The source of calcium commonly recommended is milk. And to people with whom milk agrees this is an excellent source, because milk may be consumed in such large amounts. But the calcium is not equally available in all types of milk. It has been found, for instance, that milk quickly boiled gives a retention of calcium three times as great as the slowly heated pasteurized milk, or as dried milk; and that the calcium of sweetened condensed milk can but little be assimilated. On the other hand, evaporated milk, which is recognized as good for babies, has its calcium easily available; and raw milk is best of all. The drawbacks to using raw milk are that it does not keep so well as that pasteurized, and that unless the cows furnishing it are tested with the utmost care the milk may carry the germs of tuberculosis.

Vitamin D Must Be Present to Handle the Calcium
In the skin of man there is a substance which absorbs the ultraviolet rays of sunlight. Other sterols, notably ergosterol, exist in various forms of living things. These sterols are provitamins which, when irradiated, yield vitamin D. Thus ergosterol, which is the provitamin in yeast, when irradiated becomes calciferol. Irradiated 7-dehydrocholesterol is the form in which vitamin D is found in cod liver oil and halibut liver oil and in the human skin. And this vitamin D, obtained by exposing the skin to sunlight or artificial ultraviolet light, or from foods, is absolutely essential in the maintenance of the calcium-phosphorus balance, and for the bones and nerves to utilize calcium and phosphorus.
When there is insufficient vitamin D or exposure to sunlight the system fails to assimilate calcium and phosphorus, and the parathyroid hormone draws upon the balance in the bones, weakening them, and after a time upsetting the proper balance between calcium and phosphorus, and between calcium and sodium. This not only affects the bones, but also affects the nerves and brain; for both bones and brain are dependent upon the handling of calcium and phosphorus, and nerve stability on proper neutralization of sodium and other elements by calcium.
Deficiency in vitamin D gives rise to rickets in infants; and to nervous difficulties in adults. Gould’s Medical Dictionary defines rickets thus:
“A constitutional disease of infancy, characterized by impaired nutrition and changes in the bones, the symptoms being a diffuse soreness of the body, slight fever, and profuse sweating about the head and neck, and changes in the osseous system, consisting in a thickening of the epiphyseal cartilages and periosteum and a softening of the bones.”
Where there is lack of sunlight, such as occurs in winter where the sun cannot penetrate the smoke in cities, rickets affect many children, and the adult population suffer nerve depletion. These conditions can be cured, however, by ultraviolet light or by vitamin D, provided calcium and phosphorus are present in ample amounts in the food.
Certain fish have the ability to store vitamin D. Cod liver oil has been used thus for decades in the cure of rickets. Other fish livers have the same properties but usually in less degree. Mackerel liver oil and halibut liver oil contain about half the vitamin D, white sea bass liver oil about one-third the vitamin D, and salmon liver oil about one-fiftieth the vitamin D, that is contained in cod liver oil; while the puffer fish elaborates an oil fifteen times as strong in this respect as cod.
Because the influence of the thought cells ruled by Mercury, Uranus, Neptune and Pluto when too active or discordant—as mapped by these planets in the birth chart, and at those times when progressed aspects, especially discordant progressed aspects, form involving one or more of these planets—is to weaken the secretion of parathyrin; when these planets are afflicted there is a definite need for vitamin D to enable such parathyrin as is present to handle calcium.
But vitamin D is not harmless when taken into the system in too great amounts. Excessive sunburn produces a toxic condition chiefly due to release of proteins of the tissue, but which may also be due to excessive vitamin D; and while there is no danger of getting too much vitamin D in ordinary foods, excessive dosing with vitamin D should not be encouraged as overdoses are decidedly injurious to the health.

Use Jupiter Thoughts to Neutralize Discordant Mercury or Uranus Thought-Cell Activity
While it is true that you cannot take vitamin B-1, vitamin D, or calcium into the body for parathyrin and other hormones to use in building healthy nerves and stabilizing their electromagnetic radiations, it is equally true that no matter how much, or what kind of materials you furnish the body to work with, permanently healthy nerves and stabilization of their electromagnetic radiations will not be present while the thought-cell activity mapped by Mercury, Uranus, Neptune or Pluto is too intense and discordant. Even though these thought trains are chiefly in the region of the unconscious mind, their influence will find response in the parathyroid glands and the other gland or glands which the planet mapping them rules.
All that can be done with food is to afford the optimum facilities of work for the glands and other functions. And that is a big aid; for then they will not need to work so hard to produce beneficial results. But if at the same time they are continually distressed by discordant thought-cell activity, they will find it difficult or impossible to maintain health in spite of any physical assistance that may be afforded.
Man is a two-plane organism, and for completely satisfactory results proper adjustments must be made on both planes. In addition to the foods especially needed at the time, he should provide also for beneficial thought-cell activity. And because they act as natural antidotes there is nothing better to counteract too active or discordant Uranus or Mercury thought-cell activity, and their tendency to deplete the parathyroids, than to cultivate the Jupiter attitude, placing faith in the beneficence of Divine Providence, looking confidentially to a higher than human source to oversee matters beyond control, and keeping cheerful and jovial.
Whenever the tendency to over cerebral activity is noticed, or the feeling of high tension and nervousness, a deliberate effort should be made to get into the mood of trust and faith and optimism and genial goodwill to all, which is characteristic of Jupiter thought-cell activity.
Because employed for this definite purpose, this will add the energy of the Jupiter thoughts directly to the thought cells responsible for the cerebral activity, tension or nervousness. The resulting thought-element combination is harmonious and to the extent it is thus formed will the resulting thought-cell activity relieve parathyroid strain and nerve tension and work for a healthy condition.

Influence of the Foods Upon the Disposition
I can think of no greater contrast in physiques and ideals than that between the founder of modern Germany, Bismark, the man of blood and iron, and Gandhi, the spiritual leader, who taught non-violence and freed India’s teeming millions.
Bismark (chart in Chapter 5, Serial Lesson 220) is representative in type of the American political boss, of the coarse brutality which takes no consideration of the welfare of others so long as the end is gained, and which has no sympathy for suffering. He had Leo on the Asc., Moon in Capricorn, and Sun in Aries opposition Jupiter, square Moon, sextile Mars and Saturn, and trine Uranus. In contrast to the small emaciated Gandhi, Bismark at the age of 68 weighed 247 pounds.
He was a glutton who indulged in immense amounts of highly stimulating foods all his life. Undoubtedly he indulged in food and drink to excess, and that a more moderate life would have been beneficial. But it is equally certain that a man with so high a metabolism, that is, with ability to burn so much fuel, could not have lived upon the Gandhi diet.
Gandhi (chart in Chapter 5, Serial Lesson 177, Course XX, The Next Life) had Libra on the Asc., Moon in Leo, Sun in Libra opposition Neptune, Mercury conjunction Asc., and Venus conjunction Mars in the first house, and both opposition Jupiter. In his book, “My Experiments with Truth,” Gandhi relates his experiments with food. In 1906, under progressed Sun opposition Jupiter p, he decided to become a Brahmachari which, according to the custom, required a vow of chastity in order to devote himself to a life of service to his fellow man. To keep this vow he commenced to experiment with diet in the attempt to find foods which would not excite what he terms carnal passion.
The Indian cuisine includes spices and condiments. And the general tendency of a progressed aspect involving Jupiter is to incline toward rich and highly seasoned foods. But these interfered with Gandhi’s plans to control his emotions.
After six years of experimenting he found he could attain “immunity to passion” on a diet of nuts and fruits, especially when fresh, and interlarded with days of fasting during which he took only water. Uranus is the research planet, and when progressed Sun came to the luck (trine) aspect with Uranus r, he solved his diet problem.
However, he was unable to live on this, from his point of view, most highly desirable food. He could not retain his strength upon it. Therefore, that there might be enough protein for building muscle, and thus keep him from wasting away, he had to resume drinking milk. From his standpoint, in which sexual interest was taboo, this was not desirable; for he relates that this caused a certain amount of sexual excitability and interest. As he says, “I have not the least doubt that milk diet makes the Brahmacharya (chastity) vow difficult to observe.”
Gandhi was 37 years old at the commencement of his diet experiments and 43 years old when he solved the problem, not to his satisfaction, but by a compromise between his emotional ideal and the practical requirements of life. But because Gandhi found the animal propensities even of goat’s milk to be sexually stimulating, we cannot infer that some other individual would find it so. To understand the effect of food upon the individual we must know the birth chart and progressed aspects.
The very energy which made Gandhi’s life so successful, which gave him the tremendous psychokinetic power which he possessed, was the sex energy against which he was struggling at 37 years of age.
Not only did he have Sun in the sign of marriage, Libra, and this sign on the Asc., but he had the two gonad stimulating planets, Mars and Venus, and also Mercury in the sex sign Scorpio in the house of his personality (first), Venus and Mars being in close conjunction and powerfully aspected by other planets. With thought cells such as these positions map, even at 43 and after six years of experimenting, he found even goat milk stimulated sex interest. But some other person, with Saturn in the first house, and Mars and Venus having few astrodynes, might eat almost anything and remain free from sexual desire.
Furthermore, when Gandhi in 1906 had difficulty with his desires, he had not only Sun opposition Jupiter p, inclining him to religion; but Sun conjunction Venus r, a gonad stimulating aspect. Therefore, if in his life, there was ever a need for exercising proper control over the passions, it was during the following three years while the Sun by progression made the conjunction of Venus and then Mars in his birth chart. With such aspects he required so little protein in his diet that if he had no more protein at some other period he would have found it quite inadequate.
Not to quell sexual desires perhaps, but to bring undesirable factors in our dispositions under better control, all of us are faced with the general problem which Gandhi solved by compromise. Some foods tend to increase and others decrease, the traits of disposition toward which the thought cells at birth predispose us. And when these traits are given further stimulation by progressed aspects forming which are their constants, by food selection and other environmental factors we need to make it as hard as possible for the disagreeable thought cells to find facilities for expression. For instance, when we tend to become high tension and irritable due to a progressed aspect involving Mercury or one of the upper-octave planets, we should take particular pains that we get an abundant supply of vitamin B-l, vitamin D, and calcium.
Charts



|
|