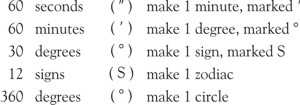To purchase the print book Horary Astrology click here

Natural Sequence of Work:  Preliminary Explanations    The Dominant Factor: Finding Local Mean Time    First Key Problem: Finding Sidereal Time of Birth     Second Key Problem: Finding E.G.M.T.I.

Tables and Charts:  Time Zone Boundary: U.S.A.    Time Zone: The World    Table of House Cusp Declinations    Example Chart 1    Table I. Signs and Their Opposites    Table II. Symbols of Planets    Table III. Table of Longitude    Table IV. Table of Time

Chapter 7

How to Erect a Horoscope (Cast a Chart)

Example Chart No. 1

IN erecting a horoscope there are simple problems of two separate kinds. The first set of problems maps the positions of the signs of the zodiac in relation to the earth. The second set of problems maps the positions of the various planets in relation to the zodiacal signs.

These problems are quite distinct from each other because the positions of the zodiacal signs are calculated from Sidereal Time, while the positions of the planets are calculated from Equivalent Greenwich Mean Time. Most of the trouble experienced by beginners arises from failing to remember that the kind of time used for mapping the zodiacal signs is not the same as the time used for mapping the planets.

Both the Sidereal Time of Birth and the Equivalent Greenwich Mean Time of Birth are derived from still a third kind of time, called Local Mean Time. Because it is necessary first to find the Local Mean Time before either of the other kinds of time can be ascertained, and therefore before either sign positions or planet positions can be computed, I call the Local Mean Time the DOMINANT FACTOR.

From this Dominant Factor, or Local Mean Time, the Sidereal Time of Birth is calculated. Because this Sidereal Time of Birth is the key to the positions of the zodiacal signs, I call Finding the Sidereal Time of Birth the FIRST KEY PROBLEM.

From this Dominant Factor, or Local Mean Time, the Equivalent Greenwich Mean Time Interval is calculated. Because this Equivalent Greenwich Mean Time Interval is the key to the positions of the planets, I call Finding the Equivalent Greenwich Mean Time Interval of Birth the SECOND KEY PROBLEM.

Yet before attempting the actual work of erecting a horoscope the student should know what a horoscope is, what data is required to erect it, the meaning of the symbols commonly employed, and how to add and subtract both Longitude and Time. These can be conveniently handled as PRELIMINARY EXPLANATIONS.

It should now be clear that erecting a horoscope divides itself according to the natural sequence of the work into four well marked divisions that are based upon) PRELIMINARY EXPLANATIONS, DOMINANT FACTOR. FIRST KEY PROBLEM, and SECOND KEY PROBLEM.

In the complete work there are eleven separate processes or steps. When you become accustomed to them some of these steps will be passed over so rapidly as hardly to be noticed; yet unless short cuts are used these eleven steps are always taken in the erection of a complete horoscope.

The time for which the chart is erected may be before noon or it may be after noon, the place may be east, or it may be west, of a standard meridian, or there may be other variations. In this one lesson I have taken into consideration all the various conditions and circumstances an astrologer is apt to meet, and have formulated rules and given examples having reference to them all. You will find twenty-seven rules.

So many rules, and the examples illustrating them, may give you the impression that erecting a horoscope is a formidable task. Yet as a matter of fact, in the erection of any one chart only a part of the rules are used. Even the following of the eleven necessary steps quickly becomes almost automatic, and you will soon do most of the calculations mentally about as quickly as you can conveniently enter the results in the map.

Instead of being a complicated task, all that is really necessary to erect a horoscope is the knowledge that the signs are placed in the map from the Sidereal Time of Birth, that the planets are placed in the map from Equivalent Greenwich Mean Time Interval of Birth, that both of these different times are computed from the Local Mean Time of Birth, and the use of addition, subtraction, and common sense.

PRELIMINARY EXPLANATIONS

The word horoscope is derived from Greek words meaning hour view. It is a map of the heavens showing the positions of the planets and zodiacal signs as viewed from some particular place at some particular time. There are, therefore, three distinct factors necessary for the erection of a horoscope of birth of a child or other event:

A—Astronomical data from which the positions of the signs and planets may be calculated.

B—The place of birth from which the heavens are to be viewed.

C—Time of birth—Year, Month, Day of Month, and Time of Day, A. M. or P. M.—when the heavens are thus to be viewed.

(A) The necessary astronomical data for calculating the positions of the signs and planets may be found in an Astronomical Ephemeris for the year of birth. Astronomical ephemerides commonly cover but a single year each, and may be had for each year since 1850.

The data for determining the relation of the heavens to the particular place may be found by consulting a table of houses for the Latitude of the place. A table of houses is good for any year, and need only approximate the latitude of birth.

Raphael’s ephemeris contains not only the positions of all the planets for mean noon, Greenwich, for each day of the year covered, but also contains an aspectarian, a table of houses for several important places, and a table of proportional logarithms.

(B) The location of the place for which the horoscope is erected may be ascertained by consulting a common atlas or geography and finding its Latitude and Longitude. Longitude is expressed in ° (degrees), ′ (minutes), and ″ (seconds) E (east) or W (west) of Greenwich. Latitude is expressed in °, ′, and ″, N (north) or S (south) of the equator. Where unusual precision is required geocentric latitude is used, but the latitude of the common map is precise enough for all ordinary purposes.

(C) There are various systems for recording time which are or have been in use. Unless the time used is known, a correct chart cannot be erected. This matter of what kind of time was used at any given date is of utmost importance, but is so complicated that it requires a special volume for treatment. Such a volume is published entitled, World Daylight Saving Time.

As the astronomical data given in the ephemeris is calculated for Mean Time, unless the time of birth is given in terms of local mean time it becomes necessary to convert the recorded time into local mean time.

The use of local mean time requires that every place having a different longitude should have a different time. As this is a nuisance, Standard Time is now used in most parts of the world. In the United States the country is divided into four Standard Time Zones each containing 15° longitude. The Standard Meridian for Eastern Time is 75°, or 5 hours, west; the Standard Meridian for Central Time is 90°, or 6 hours, west; the Standard Meridian for Mountain Time is 105°, or 7 hours, west; and the Standard Meridian for Pacific Time is 120°, or 8 hours, west. Eastern Canada has a further zone, called Atlantic Time, which is but 4 hours west.

Time Zone Map: USA

Theoretically, all places 7½° east and 7½° west of a standard meridian should keep the same time. As a matter of fact, railroad divisions and natural boundaries greatly influence the actual place where time changes are made. Furthermore, the dividing line where such changes of time take place has not remained constant, but has shifted along with railroad changes and the development of certain regions. The map on page of this chapter (Serial Lesson 86), gives the zones and places of time change as they exist at the present time. But if a birth is near these places of time change, much pains should be exercised to ascertain just what time was used in recording the birth.

Standard Time was adopted throughout the United States, theoretically, Nov. 18, 1883, at noon; and in Great Britain in 1880. Actually it was not used in many places until considerably later. Previous to these dates each place used its own time, the Local Mean Time. On all dates after the adoption of Standard Time, when the time given is that of the ordinary watch or clock, it becomes necessary to convert this standard Time to Local Mean Time.

To still further complicate matters, during and following the great war, daylight saving time was adopted in many countries. It was in general use in the U. S. during 1918 and 1919, and is still used in some sections of the country. As if this were not confusion enough, in some towns in the eastern U. S. at the present, there are two kinds of time in use. Daylight Saving Time has been made legal, but as it so complicates schedules, the railroads continue to use Standard Time. To get the time of birth right, inquiry must be made as to which time was used in the record.

The U. S. used Daylight Saving in 1918 from March 31 to October 27, and in 1919 from March 30 to October 26 but where continued the change date varies. When the birth is timed by Daylight Saving, it becomes necessary to subtract one hour from the clock time to get the Standard Time. Then in the usual way, Standard Time may be converted into Local Mean Time.

Then again, in some countries, notably Russia, the Julian Calendar was used up to the time of the Revolution in 1917. Even here there are exceptions, as some places on the Black Sea used the calendar of their neighbors. When, however, the date is given Old Style, as it was reckoned in Russia, it must be converted into the Gregorian Calendar, or New Style, because the ephemeris is calculated New Style. This is done by adding 12 days to Old Style dates occurring in the 19th Century, and by adding 13 days to Old Style dates since 1900. Thus, Jan. 2, 1916, Old Style, is the same as Jan. 15, 1916, New Style. The horoscope, consequently, should be erected for Jan. 15.

How to Recognize Astronomical Symbols, and the Signs that Always Occur Opposite Each Other

Rule 1. To add Long. or R.A.

Add the ″, and if the sum exceeds 60″ subtract 60″ from it, the remainder being ″ and each 60″ being called 1′ and added to the ′ column. Add the ′ including that carried over from the column and if the sum exceeds 60′, subtract 60′ from it, the remainder being ′ and each 60′ being called 1° and added to the ° column. Add the °, including that carried over from the ′ column, and if the sum exceeds 360° subtract 360 from it. The remainder being °, and each 360° being called a circle and discarded.

Example (1). Given Perth, W. Australia, with a long. 115° 54′ E. and St. Johns, Newfoundland, with a long. 52° 42′ W to find how far in long. they are apart.

Rule 2. To subtract Long. or R.A.

Subtract ″ from ″, and if the minuend be too small, borrow 1′ from the ′ column, and calling it 60″ add to the minuend ″ column. Subtract ′ from ′, and if the minuend be too small borrow 1° from the ° column and calling it 60′ add to the ′ in the minuend. Subtract ° from ° and if the minuend be too small add the full circle of 360° to the ° in the minuend to make subtraction possible.

Example (2). Traveling in a westerly direction from San Francisco with a long. of 122° 26′ W., how far is it in long. to Buenos Aires with a long. of 58° 18′ W.?

Table 4: Table of Time

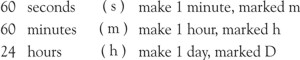
Mean Time and Sidereal Time are expressed in h (hours), m (minutes), and s (seconds). Table IV (above), giving this, should be memorized.

Rule 3. To add Mean Time

Proceed as in adding long. except that if the total sum exceeds 12h, 12h should be subtracted from it, calling the difference P.M. of the same day if A.M. was given, or A.M. of the following day if P.M. was given.

Example (3a). Given a mean time of 11h 58m 32s A.M. Jan. 6, to find the mean time 6h 23m 52s later.

Example (3b). Given a mean time of 10h 24m 31s P.M. Jan, 6, to find the mean time 8h 42m 35s later.

Rule 4. To subtract Mean Time

Proceed as in subtracting long. except that if the minuend be too small in h, 12h must be added to it, and the difference is then P.M. of the day before if A.M. time is given, or A.M. of the same day if P.M. time is given.

Example (4a). Given a mean time of 8h 42m 36s A.M. Jan. 6, to find the mean time 10h 38m 56s earlier.

Example (4b). Given a mean time of 7h 37m 22s P.M. Jan. 6, to find the mean time 9h 21m 58s earlier.

Rule 5. To add or subtract Sidereal Time (S.T.)

Proceed as with mean time except that when the sum is in excess of 24h, 24h must be subtracted, the remainder being the required S.T.; and when the minuend is too small to permit subtraction, 24h must first be added to it.

Example (5a). Given a S.T. of 19h 24m 29s. to find the S.T. 6h 4m 31s later.

Example (5b). Given a S.T. of 4h 27m 18s, to find the S.T. 5h 41m 28s earlier.

Rule 6. To add Zodiacal Longitude

Proceed as in geographical longitude except that if the sum exceeds 30°, subtract 30° from it, each 30° being called One Sign and added to the sign column. If the signs exceed 12, subtract 12S from the sum, being careful to note that Pisces is both sign 12, and sign 0.

Example (6). Given Pisces (12S) 28° 4′ 29″. to add 4° 16′ 33″ to it.

Rule 7. To subtract Zodiacal Longitude

Proceed as in subtracting geographical longitude except that if the minuend be too small in S, 12S must be added to it, and if too small in °, 30° (1S) must be borrowed from the S column.

Example (7). Given Aries 4° 32′ 16″, to subtract 20° 33′ 19″ from it.

THE DOMINANT FACTOR

STEP I. How to Find the Local Mean Time

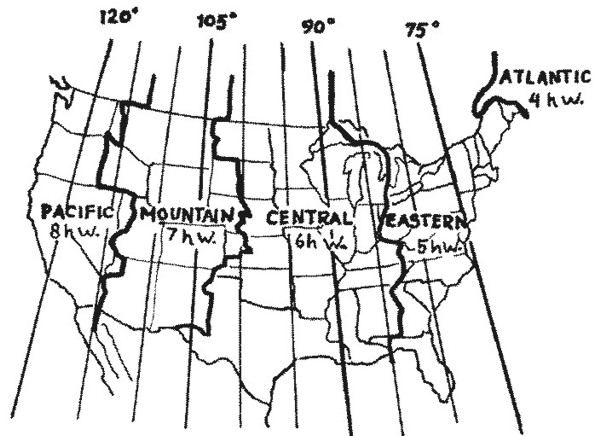
One complete revolution of the earth on its axis, which is the time between two successive transits of the sun’s semi-diameter across the same meridian, measures 24 hours. In the complete revolution the 360° of geographical longitude measuring the earth’s circumference pass under the sun at meridian. Dividing 360° by 24, gives 15° that pass under the sun at meridian every hour. Dividing this hour of 60 minutes by 15 gives 4 minutes as the time required for 1° longitude to pass under the sun at meridian.

Thus in the prevalent method of reckoning, the Standard Meridians of Time, starting at Greenwich, are exact multiples of 15° E. or W., there being a difference of just 1h in time between successive Standard Meridians. A glance at the map below will indicate these various meridians and time zones.

Time Zone Map: World

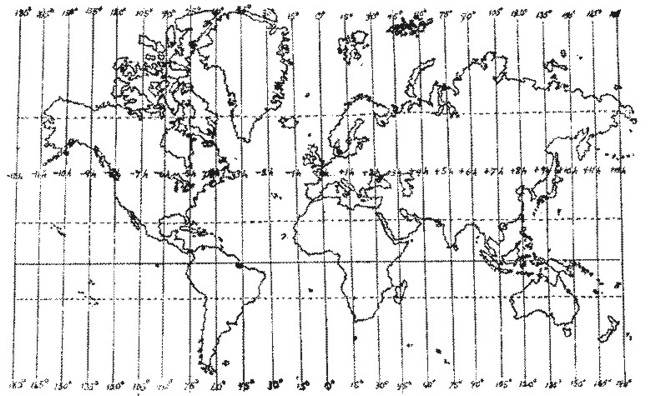
Now if the place for which the chart is to be erected is exactly on one of the Standard Meridians the Local Mean Time (L.M.T.) is the same as the time recorded by the clock. But since standard time came into use, if the place is either E. or W. of a standard meridian, the clock time must be converted into L.M.T.

Clocks west of a Standard Meridian are FAST. Clocks east of a Standard Meridian are SLOW. And as 1° longitude is the equivalent of 4m time, as shown above, the number of ° E. or W. of the Standard Meridian may be converted into time merely by multiplying by 4 and calling the result minutes.

Rule 8. When Standard Time is given to find the L.M.T. at a place WEST of a Standard Meridian

Multiply the ° distant from the standard by 4, calling the result minutes, multiply the minutes by 4 to get seconds, and subtract from standard time.

Example (8). Given a standard time at San Francisco of 5h 00m A.M., to find the L.M.T. San Francisco is 122° W. 26″ long. The Pacific Standard Meridian is 120° W. Difference in long. is 2° 26′.

2° 26′ x 4 gives 9 minutes 44 seconds.

Rule 9. When Standard Time is given to find the L.M.T. at a place EAST of a Standard Meridian

Multiply the ° distant from the standard by 4, calling the result minutes, the minutes by 4 to get seconds, and add to the standard time.

Example (9). Given a standard time at New York of 5h 32m P.M., to find the L.M.T. New York is 73°W. 57′ long. The Eastern Standard Meridian is 75° W. 00′. Difference in long. is 1° 3′.

1° 3′ x 4 gives 4 minutes 12 seconds.

SIGNS ON HOUSES

STEP II. How to Find the Sidereal Time of Birth

FIRST KEY PROBLEM

The celestial equator is the projection of the earth’s equator in the heavens. There are 360° in the celestial equator. To measure any circle a starting point is necessary. The starting point for measuring along the earth’s equator is the Meridian of Greenwich. The starting point for measuring along the celestial equator is the point where the sun crosses it each year moving north in the spring of the year. This point is the vernal equinox called 0° Aries.

The distance E. or W. of Greenwich as we have seen may be expressed in °, ′, and ″, or in h, m, and s. So, likewise, the distance E. or W. of 0° Aries may be expressed in °, ′, and ″, and so expressed is called Right Ascension (R.A.). Or it may be expressed in h, m, and s, and then is called Sidereal Time (S.T.). R.A. in the heavens corresponds to geographical longitude. Sidereal Time is the distance along the celestial equator from 0° Aries expressed in Time. The S.T. at noon of any day represents the distance of the point on the celestial equator from 0° Aries that is on the Mid Heaven (M.C.) at noon of that day.

Knowing the S.T.—distance from 0° Aries in time—on the M.C. at noon, and that the whole celestial equator must pass the M.C. in 24h, it is easy to calculate the S.T.—distance from 0° Aries—that is on the M.C. at any moment of that day. The INTERVAL of time since noon added to the S.T. at noon, or the INTERVAL of time before noon subtracted from the S.T. at noon, must give the required S.T. This is the exact distance of the point on the M.C. from 0° Aries.

The Sidereal Time at noon for each day at Greenwich is given in the ephemeris for the year in which the date occurs.

Rule 10. To find the Sidereal Time when the L.M.T. is after noon

Consult the ephemeris for that year and day and to the S.T. there given for noon add the L.M.T., or INTERVAL after noon. For greater precision see correction below.

Rule 11. To find the Sidereal Time when the L.M.T. is before noon

Consult the ephemeris for that year and day and from the S.T. there given for noon subtract the INTERVAL between the L.M.T. and noon. For greater precision see correction below.

Correction of Sidereal Time for Precision

As Sidereal Time increases at the rate of approximately 4 minutes a day where precision is required a correction of 9.86s (roughly 10s) per hour must be made both for longitude from Greenwich, and for the INTERVAL between L.M.T. and noon. The separate correction for L.M.T. is best performed by always ADDING 9.86s per hour to the INTERVAL between L.M.T. and noon. The separate correction for longitude may best be performed by adding 9.86s per hour to S.T. if west, and subtracting 9.86s per hour from S.T. if east, longitude.

It is easier in actual practice to make BOTH corrections at one operation after finding the E.G.M.T. INTERVAL (Step IV) by adding 9.86s per hour that the INTERVAL E.G.M.T. is past noon to the S.T., or subtracting 9.86s per hour that the INTERVAL E.G.M.T. is before noon from the S.T. See Chapter 8 (Serial Lesson 36), “Chart Erection Short Cuts and Examples.”

For the sake of clearness of detail the examples here perform the two corrections separately.

Example (10). Given a L.M.T. of 5h 36m 12s P.M. Jan. 2, 1920, at New York, to find the Sidereal Time.

Example (11). Given a L.M.T. of 4h 50m 16s A.M. March 4, 1920, at San Francisco, to find the Sidereal Time.

STEP III. How to Place Signs and Degrees Upon House Cusps

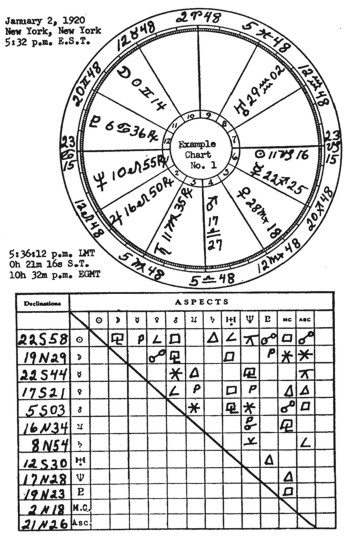
The dividing line between one house and another is called its cusp. The houses are numbered in example chart No. 1 (top of page).

Rule 12. In a table of houses for the latitude of birth find in its column the S.T. of birth.

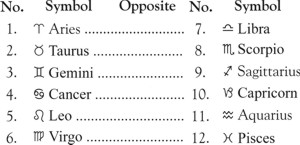
Opposite this time, or its nearest approximate, will be found the sign and degree to be placed on each house cusp from 10th to 3rd. When these have been entered into the chart on their appropriate cusps, place the same degree of the opposite sign on the opposite house cusp. Signs opposite each other are given in Table I (page ).

Example (12). Given a S.T. of Birth at New York of 0h 21m 16s, to place the zodiacal signs and degrees in the chart.

New York is 40° 43′ N. Latitude. Consulting the table of houses for this latitude given in Raphael’s ephemeris I find the nearest S.T. given as 0h 22m 02s. Opposite this S.T. under column marked 10, I find 6°, and looking up this column I find this to be of the sign Aries. I therefore place 6° Aries on the cusp of the 10th house in the chart.

Opposite the same S.T. I find 13° Taurus on the 11th house cusp, 21° Gemini on the 12th house cusp, 23° 24′ Cancer on the 1st house cusp, or Ascendant, 13° Leo on the 2nd house cusp, and 6° Virgo on the 3rd house cusp. And I place them thus in the chart.

For the 4th house cusp I look in Table I of opposite signs and as Libra is always opposite Aries I use 6° Libra. For the 5th house cusp I use 13° Scorpio, as Scorpio is opposite Taurus; on the 6th I use 21° Sagittarius because Sagittarius is opposite Gemini; on the 7th I use 23° 24′ Capricorn because Capricorn is opposite Cancer; on the 8th I use 13° Aquarius because Aquarius is opposite Leo; and on the 9th I use 6° Pisces because Pisces is always opposite Virgo. Example chart No. I has been corrected by Rule 13.

Inserting Missing Signs

Frequently the same sign will be found on more than one house cusp. When this occurs other signs are missing. These may be found by counting the signs in their regular order. They should then be entered on the map in the middle of those houses where they fall by their natural sequence in the zodiac.

Tables of houses may be had giving the house cusp to the nearest tenth of a degree. Where great precision is required the exact minute on any house cusp may be found by the following rule:

Rule 13. To find the exact ′ on any house cusp**:

**(For mapping the character, and the type of events which the thought-cells so mapped tend to attract, a chart with the nearest degree on the Ascendant and Midheaven is precise enough. But when it is desired to progress the positions of the chart to determine WHEN energy from a certain planet will be added to a group of thought-cells in sufficient volume to attract a specific event, it is essential that the Ascendant and Midheaven, which are treated as planets, should be calculated to the exact minute of zodiacal longitude.)

Look in a table of houses for the latitude of birth. Find (a) the difference between the nearest and the next nearest S.T. of birth. Find (b) the difference between the True S.T. of birth and the nearest S.T. of birth. Find (c) the difference between the cusps corresponding to the nearest and the next nearest S.T. of birth. Then (a): (b) :: (c): ?

Multiply (b) by (c) and divide the product by (a). If the True S.T. of birth is more than the nearest S.T. add; if less, subtract.

Example 13. To find the exact ′ on the Ascendant when the S.T. of birth at New York is 0h 21m 16s.

To Work a Problem In Proportion

As the product of the means is equal to the product of the extremes, when the two inner terms are given multiply one by the other and divide the product by the outer term. When the two outer terms are given multiply one by the other and divide the product by the inner term. The result is the answer. Such problems are taught in grammar school, and are essential to astrological work.

221 (a) : 46 (b) :: 44 (c) : ?

44 X 46 equals 2024

2024 divided by 221 equals 9′

South Latitude

Tables of houses for north latitude may be used for places in south latitude by adding 12h to the S.T. and using the degrees thus found, but placing opposite signs on the house cusps. Detailed examples of this will be found in Chapter 8 (Serial Lesson 36), “Chart Erection Short Cuts and Examples.”

PLANETS IN SIGNS

STEP IV. How to Find the E.G.M.T. INTERVAL

SECOND KEY PROBLEM

Rule 14. To find the difference in time between the place of birth and Greenwich multiply the ° distant in longitude from Greenwich by 4, calling the product minutes, and multiply the ′ by 4, calling the product seconds. Convert into hours and minutes.

Example (14). Given a long. of 73° W 57′ (New York) to find the difference in time from Greenwich.

73 x 4 equals 292m. 57 x 4 equals 228s. 292m divided by 60 equals 4h, plus 52m remainder. 228s divided by 60 equals 3m, plus 48s remainder. 4h 52m plus 3m 48s equals 4h 55m 48s. Ans.

Rule 15. Divide the ° by 15. The quotient is hours, the remainder multiplied by 4 is minutes.

Example (15). Given a long. of 118 ¼ ° (Los Angeles) to find the difference in time from Greenwich.

118¼ divided by 15 equals 7h. The remainder, 13¼ x 4 equals 53m. 7h 53m, Ans.

Rule 16. To find the E.G.M.T. when the place is west of Greenwich add the difference in time to the L.M.T., when the place is east of Greenwich subtract the difference in time from the L.M.T.

Example (16a). Given a L.M.T. of 5h 36m P.M. and a difference in time of 4h 56m W. (New York), to find the E.G.M.T.

Example (16b). Given a L.M.T. of 10h 02m A.M., and difference in time of 54m E. (Berlin), to find the E.G.M.T.

Example (16c). Given a L.M.T. of 4h 50m A.M., and difference in time of 7h 53m W. (Los Angeles), to find the E.G.M.T.

The Interval E.G.M.T. is the number of hours and minutes after noon, called a PLUS INTERVAL, or the number of hours and minutes before noon, called a MINUS INTERVAL.

Thus in the above examples the E.G.M.T. Interval of (a) is plus 10h 32m, of (c) is plus 0h 43m. But if the E.G.M.T. is before noon, it must be subtracted from noon to get the Interval, and the result is then a Minus Interval. Thus in the above example (b) find the Interval.

STEP V. How to Find the Constant Proportional Logarithm

A table of proportional logarithms is a decimal mathematical table simplifying difficult problems in proportion. The Constant Logarithm is the number found in a table of proportional logarithms corresponding to the E.G.M.T. Interval.

Rule 17. To find the Constant Logarithm

Look in a table of diurnal proportional logarithms and find the figure corresponding to the E.G.M.T. Interval.

Example (17). Find the Constant Log. for an interval of plus 10h 32m. Interval is 10h 32m. Looking in the table of proportional logarithms in the back of Raphael’s ephemeris I look down the column marked 10h until it intersects with the horizontal column marked 32m. There I find .3576. Ans.

STEP VI. How to Find the Daily Motion of Any Planet

In recent years the swifter planets have their daily motion given for each day in the latter part of Raphael’s Ephemeris.

Rule 18. To find the daily zodiacal motion of any planet

Consult the ephemeris for the two days between which the E.G.M.T. occurs and subtract the less longitude from the greater in the regular order of the zodiacal signs.***

***Pluto’s position is given in Raphael’s ephemeris starting 1934, and in the Pluto ephemeris for earlier years. Call the days between ephemeris positions (a), the days between ephemeris date and required date (b), the minutes Pluto moves between these two positions (c), and the motion of Pluto during required interval (d). Then (a): (b) :: (c) (d).Thus using the Pluto ephemeris, during the 30 days (a) from December 16, 1919, to January 15, 1920, Pluto moves 35′ (c). The interval between January 2 and January 15 is 13 days (b). 35 multiplied by 13 and divided by 30 gives 15′ as the motion of Pluto during this interval. As it is retrograde, add these 15′ to the place of Pluto January 15, and it gives the longitude of Pluto January 2, 1920, as 6 Cancer 36 R.

Example (18). Find the daily zodiacal motion of the Moon Jan. 2, 1920.

Rule 19. To find the daily declination motion of any planet

Consult the ephemeris for the two days between which the E.G.M.T. occurs, and if both are either N. or S. declination subtract the less from the greater; but if one is N. and the other S. declination, add the given declinations. If the declination is given only every 2nd or 3rd day the result must be divided by 2 or by 3 to get the daily motion.

Example (19a). Find the daily declination motion of Mercury Jan. 2, 1920.

Example (19b). Find the daily declination motion of Venus Apr. 14, 1920.

STEP VII. How to Find the Proportional Logarithm of the Daily Motion of a Planet

Rule 20. To find the proportional logarithm of a planet’s daily motion

Look in a table of proportional logarithms and find the ° and ′ corresponding to its daily motion.

Example (20). Find the prop. Log. of the Moon’s daily notion Jan. 2, 1920. Daily motion (example 18) 14° 48′ 9″. Neglecting the 9″ I consult the table of logarithms in Raphael’s ephemeris and where the column 14° intersects with 48′ I find .2099. Ans.

STEP VIII. How to Find the Motion of Any Planet for the E.G.M.T. Interval

Rule 21. To find the distance traveled by any planet during the Interval

Add the Constant Logarithm to the Logarithm of the Daily Motion. This gives the log. of distance traveled during the Interval.

Example (21). How far in longitude does the Moon travel on Jan. 2, 1920, during a plus interval of 10h 32m?

Looking in table of logarithms I find that .5675 gives 6° 30′ which is the Answer.

Note: In using logarithms always use the nearest approximate figure.

STEP IX.

To Find the Zodiacal Longitude of the Planets at Birth

Rule 22. To find the zodiacal longitude of a planet when the Interval is plus

Add its travel for the interval to the place given in the ephemeris for noon. When the Interval is minus, subtract its travel for the interval from the place given in the ephemeris for noon. If, however, the planet is retrograde (marked R at top of column in ephemeris) reverse this, and subtract for plus interval, and add for minus interval.

Example (22). Find the zodiacal longitude of the Moon Jan. 2, 1920, when there is a plus E.G.M.T. Interval of 10h 32m.

STEP X.

To Find the Declination of the Planets at Birth

Rule 23. To find the declination of a planet when the Interval is plus

Add the declination for the interval to the noon declination if the declination is increasing, subtract if decreasing. When the Interval is minus, subtract the declination for the interval from the noon declination if the declination is increasing, add if decreasing. If the declination changes from N to S or S to N, this must be allowed for.

Example (23). Find the declination of the Moon Jan 2, 1920, when there is a minus Interval of 2h 14m

The declination of any house cusp, the Moon’s Nodes, or the Part of Fortune is always that of the Sun when it is in the same sign and degree.

Rule 24. To find the declination of any house cusp, the Moon’s Nodes, or the Part of Fortune

Look in the ephemeris for the position of the Sun in the same sign, degree and minute, and use this declination.****

****Declination of the Angles: Find (a) difference between nearest and next nearest longitude in table. Find (b) difference between nearest long. in table and long. of Angle. Find (c) difference between declinations corresponding to nearest and next nearest long. in table. Problem by Logs: (b) minus (a) plus (c) equals (d) correction to be made. Add correction to nearest decl. in table if nearest long. is smaller than long. of Angle; if larger, subtract.

Subtracting 3′ from 21° N29′ gives 21°N26′ as the Answer.

Table of House Cusp Declinations

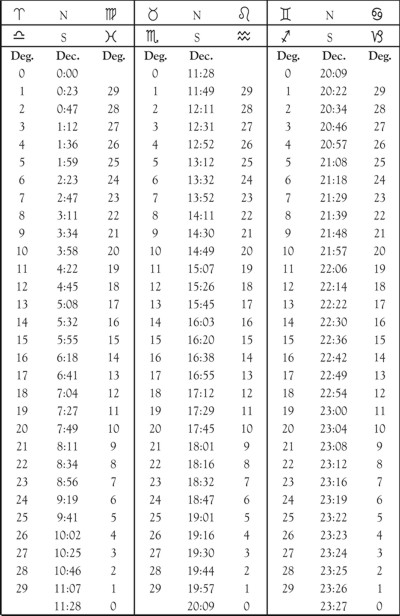
Example (24). Find the declination of the Ascendant when Cancer 23° 37′ is rising.

July 16, 1920, shows the Sun in Cancer 23° 37′, and on that day it also has declination N 21° 23′, which is the Answer.

STEP Xa.

How to Find the Zodiacal Longitude of the Fixed Stars, the Dragon’s Head and Tail, and the Part of Fortune

The zodiacal positions of the fixed stars may be had from tables made for that purpose. As they move only 1 ° in about 72 years their places may be had by inspection. The house positions of the stars, however, for those having considerable latitude, require the use of trigonometrical calculations.

Example: What important Fixed Star is nearest the Asc. in longitude when Cancer 23° 13′ rises? Looking in Dalton’s “Sixteen Principle Stars” I find on Jan. 2, 1920, the star Procyon in Cancer 24° 41′ 8″.

The Dragon’s Head is the Moon’s north Node, the Dragon’s Tail is its south Node. The North Node is calculated from its place as given in the ephemeris as if it were a planet, and the South Node is always the same degree of the opposite sign.

Example: Find Moon’s Nodes for Jan. 2, 1920, for a plus E.G.M.T. Interval of 10h 32m. Looking in ephemeris for Jan. 2, I find the North Node in Scorpio 22° 17′ . The South node, therefore, is Taurus 22° 17′ .

The Part of Fortune is a point on the ecliptic (zodiac) as far removed from the Ascendant by longitude as the Moon is removed from the Sun by longitude.

Rule 25. To find the Part of Fortune

From the sum of the zodiacal longitudes of the Ascendant and Moon subtract the zodiacal longitude of the Sun. This difference is the longitude of the Part of Fortune.

Example (25). Find the Part of Fortune Jan. 2, 1920, for a plus E.G.M.T. Interval of 10h 32m.

STEP XI.

How to Place the Planets in the Chart

Rule 26. The declination of each planet N. or S. having been calculated, it should be placed opposite its symbol in a column at one side of the chart.

See Example Chart No. 1 (top of page).

Rule 27. The zodiacal longitude of each planet having been calculated, start with the Ascendant.

Remember the degrees recorded are those above the horizon in this case, hence if a planet has less degrees of the same sign it must be placed above the house cusp in the 12th, but if it has more degrees it must be placed in the chart below the Asc. Then proceed around the chart in the order of sequence of the houses entering the planets in their signs, placing those having less degrees than the house cusp next back toward the Ascendant, and those having more degrees than the house cusp in the house farther removed from the Asc. following the proper order of sequence of houses.

The Moon’s Nodes, Part of Fortune, and Fixed Stars having little latitude may be placed in the chart in the same manner. Fixed Stars having much latitude must be entered by R.A. and Dec. (See Dalton’s Fixed Stars.)

As in thousands of birth charts erected and progressed to the date of some event, The Brotherhood of Light Research Department has found no instance where a Fixed Star, he Moon’s Nodes, or the Part of Fortune has been required to explain either the character of an individual or any event that has happened to him, we make no use of them. It must be remembered that the positions in a chart of Uranus, Neptune and Pluto were unknown to earlier astrologers, who doubtless became aware of influences apart from the seven naked eye orbs, and accounted for them as best they could.

To purchase the print book Horary Astrology click here